Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 96

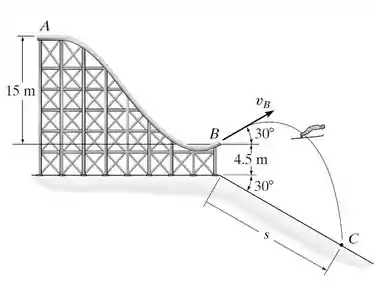
O esquiador de 65   kg parte do repouso em A. Determine sua velocidade em B e a distância s onde ele pousa em C. Despreze o atrito.

Passo 1

De acordo com os dados da figura do problema, a conservação de energia pode ser expressa tendo o ponto A como referência da seguinte forma

E C A + E g A =   E C B + E g B

1 2 m v A 2 + g m h A =   1 2 m v B 2 + g m h B

0 + 0 = 1 2 65 v B 2 + ( 65 ) ( 9,81 ) ( - 15 )

v B = 17,16   m / s   = 17,2   m / s

Passo 2

Considerando o movimento na direção x temos,

s x = s B x + v B x t

s c o s 30 ° = 0 + 17,16 s i n ⁡ ( 30 ° ) ( t )

s = 17,16 t

Considerando o movimento na direção y temos,

s y = s B y + v B y t + 1 2 a y t 2

- ( 4,5 + s s i n 30 ° = 0 + 17,16 sin ⁡ 30 ° t + 1 2 ( - 9,81 ) t 2

0 = 4,5 + 0,5 s + 8,5776 t - 4,905 t 2

Passo 3

Resolvendo o sistema

s = 17,16 t 0 = 4,5 + 0,5 s + 8,5776 t - 4,905 t 2

Substituindo a primeira equação na segunda

0 = 4,5 + 17,16 t - 4,905 t 2

Temos as seguintes raízes da equação do segundo grau

t = - 0,2507

t = 3,74  

Como o tempo sendo positivo para esse problema é a única soluçao aplicavel, o deslocmento s é,

s = 17,16 3,74 = 64,2   m

Resposta

A velocidade em B é 17,2   m / s e a distância s é 64,2   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os carros de uma atração de um parque de diversões têm uma velocidade v 1 = 90k m / h na parte mais baixa do trilho. Determine sua velocidade v 2 na parte mais alta do trilho. Despreze as perdas de er
Um satélite artificial que se desloca em uma órbita eliptica tem uma velocidade de 25000k m / h a uma altitude de 2200m no ponto A . Determine sua velocidade v B no ponto B onde a altitude é 2500k m .
Uma partícula se encontra sob a influência de uma força F = - k x + k x 3 α 2 , onde k e α são constantes e k é positivo. Determine U(x) e discuta o movimento. O que ocorre quando E = (1/4)kα2?
De acordo com a relatividade especial, uma partícula de massa m0 em repouso, acelerada em uma dimensão por uma força F, obedece a equação de movimento dp/dt = F. Nesse caso, p = m0v/(1 – v2/c2) é a qu
Uma partícula de massa m se movimentando em uma dimensão tem energia potencial U(x) = U0[2(x/a)2 – (x/a)4], onde U0 e a são constantes positivas.Determine a força F(x) atuando sobre a partícula.Faça u