Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 40
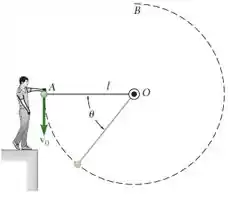
A esfera em é empurrada para baixo com velocidade de intensidade 5 m/s e oscila em um plano vertical na extremidade de uma corda de comprimento , presa a um apoio em . Determine o ângulo no qual a corda irá romper-se, sabendo que ela pode resistir a uma tração máxima igual ao dobro do peso da esfera.
Passo 1
Vamos lá! Como estamos em um capítulo que trabalha com trabalho e energia, vamos utilizar esta metodologia para resolver esta questão! Assim, vamos começar identificando cada um dos termos para aplicarmos este princípio.
No ponto inicial, a esfera possui uma velocidade . Já no ponto final, ela terá velocidade (que nada sabemos ainda). Portanto, as energias cinéticas são:
E como a única força a qual a esfera está submetida é a força peso, o trabalho desta força sobre a esfera será:
Portanto, pelo princípio de trabalho e energia, temos:
E chegamos assim a uma equação com duas incógnitas ( e ). Precisamos de outra equação para montarmos um sistema e descobrirmos quem é o ângulo (na real a gente descobre o seno, mas aí saí o automaticamente!).
Passo 2
Agora, vamos ter que utilizar a informação de que a corda se rompe quando a tração for duas vezes o valor do peso. Mas para isto, será necessário fazemos o diagrama de corpo livre da esfera. Portanto, temos:
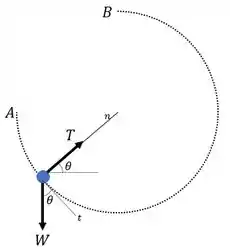
A ideia aqui é descobrir qual o ângulo cuja tensão de tração será igual ao dobro do peso, isto é, .
Como a esfera está em um movimento circular, temos então a presença de uma força centrípeta. Fazendo o somatório das forças na direção normal a curva, temos:
E assim chegamos a nossa segunda equação com duas incógnitas!
Passo 3
Agora só nos resta resolvermos o nosso sistema de equação. Relembrando-o, temos:
Agora é fácil! Basta substituirmos a segunda equação na primeira e desenvolvermos. Portanto,
E assim finalizamos a nossa questão!