Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 37
O simulador de voo é montado sobre seis atuadores hidráulicos conectados em pares aos seus pontos de fixação na parte inferior do simulador. Por meio da programação das ações dos atuadores, uma variedade de condições de voo pode ser simulada com deslocamentos de translação e de rotação ao longo de uma faixa limitada de movimentos. Os eixos estão presos ao simulador, com origem no centro do volume. Para o instante representado, possui uma velocidade e uma aceleração na direção horizontal de 0.96 m/s e 1.2 m/s², respectivamente. Simultaneamente, as velocidades angulares e suas taxas de variação no tempo são , , , , . Para esse instante, determine os módulos da velocidade e da aceleração do ponto .
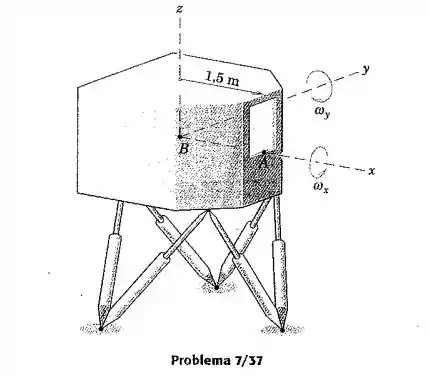
Passo 1
Para esse problema vamos usar as relações de velocidade e aceleração relativa de um ponto além dos dados que o problema nos dá.
Passo 2
Vamos começar calculando a velocidade do ponto . Temos pela relação que
E que , e
Calculando o produto vetorial, chegaremos no seguinte valor:
Substituindo os valores em chegamos que
Passo 3
Para a aceleração do ponto agora, temos que
Onde , .
Calculando os valores, temos que
Substituindo os valores, chegamos então que