Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 43
O bloco A tem uma massa e está ligado a uma mola tendo uma rigidez k e comprimento não deformado . Se outro bloco B, tendo uma massa , é pressionado contra A de maneira que a mola deforme uma distância d, mostre que para a separação ocorrer é necessário que , onde é o coeficiente de atrito cinético entre os blocos e o solo. Além disso, qual é a distância que os blocos deslizam sobre a superfície antes de se separarem?
Passo 1
Começaremos o exercício esquematizando os diagramas de corpo livre para os blocos A e B, respectivamente:
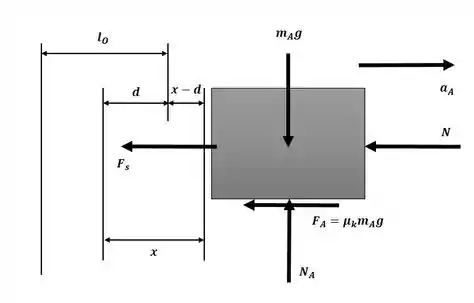
Aplicando o somatório de forças na direção x para o bloco A:
Agora para o bloco B:
Passo 2
Uma vez que os blocos possuem a mesma aceleração , podemos igualar as duas relações encontradas:
Isolando a:
Agora subsituindo esse valor na relação entre a e N encontrada no passo 1:
Sendo assim, temos que quando
Passo 3
Agora iremos integrar a relação para descobrir o valor da velocidade nesse instante:
Para atender as condições do enunciado, a velocidade deve ser maior que zero, logo:
Resposta
Ei, a resposta está no passo a passo :)