Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 80

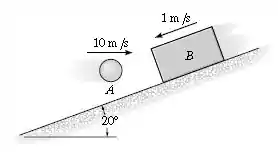
A bola de 2   k g é lançada de modo a se mover horizontalmente a 10   m / s quando atinge o bloco de 6   k g , que está descendo o plano inclinado a 1   m / s . Se o coeficiente de restituição entre a bola e o bloco é e = 0,6 , e o impacto ocorre em 0,006   s e g u n d o s ,   determine a força impulsiva média entre a bola e o bloco.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Bom galera... para determinar as velocidades após o impacto, temos que aplicar a conservação de movimento linear:

+ ↗     ∑ m 1 v 1 = ∑ m 2 v 2

2 10 cos ⁡ 20 ° - 6 1 = 2 v A x 2 + 6 v B x 2

v A x 2 + 3 v B x 2 = 6,3969

Podemos aplicar o conceito de restituição para encontrar outra equação que nos ajude a resolver o sistema:

e = v B x 2 - v A x 2 v A x 1 - v B x 1

0,6 = v B x 2 - v A x 2 10 cos ⁡ 20 ° - ( - 1 )

v B x 2 - v A x 2 = 6,23816

Podemos somar as duas equações que achamos:

v B x 2 - v A x 2 + v A x 2 + 3 v B x 2 = 6,23816 + 6,3969

4 v B x 2 = 12,63506

v B x 2 = 3,1588   m / s       ↗

Logo:

v A x 2 + 3 3,1588 = 6,3969

v A x 2 = - 3,0795   m / s

v A x 2 = 3,0795   m / s       ↙

Passo 2

Sabemos que o bloco B, não terá componente da velocidade em y , pois ele tende a seguir o a rampa que consideramos como a nossa componente x . Portanto:

v B 2 = 3,1588   m / s

O diagrama de corpo livre do sistema é:

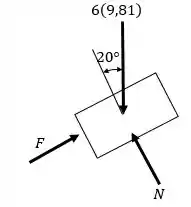
Onde F é a força impulsiva que A , provoca em B . Aplicando o principio da quantidade de movimento e impulso, temos:

+ ↗   m v 1 + ∑ ∫ F d t = m v 2

- 6 1 + F 0,006 = 6 ( 3,1588 )

F = 4,16   k N

Resposta

F = 4,16   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bala de 60g é disparada horizontalmente com uma velocidade v 1 = 600m / s contra o bloco de 3k g de madeira macia inicialmente em repouso sobre a superfície horizontal. A bala emerge do bloco com
O bloco de 9k g está se deslocando para a direita com uma velocidade de 0,6m / s sobre uma superfície horizontal quando uma força P é aplicada a ele no instante de tempo t = 0 . Calcule a velocidade v
Um vagão ferroviário de massa m e velocidade inicial v colide e se acopa com os dois vagões idênticos. Calcule a velocidade final v ' do grupo de três vagões e a fração n de perda de energia se (a) a
O vagão de carga A com uma massa total de 80t está se deslocando ao longo do trilho horizontal em um pátio de manobras a 3k m / h . O vagão de carga B com uma massa total de 60t e se deslocando a 5k m
A velocidade de uma partícula de 1,2k g é dada por v → = 1,5 t 3i ^ + 2,4 - 3 t 2 j ^ + 5k ^ , onde v → é expresso em metros por segundo e o tempo t é expresso em segundos. Determine a quantidade de m