O bloco triangular de peso se apoia sobre os cantos lisos que estão separados por uma distância . Se o bloco possui três lados iguais de comprimento , determine o ângulo para que haja equilíbrio.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o ângulo necessário para que o corpo esteja em equilíbrio. Considerando que o bloco triangular tem peso e se apoia nos cantos lisos e separados por uma distância .
Então bora lá! Para resolver esse problema, vamos começar analisando o diagrama de corpo livre:
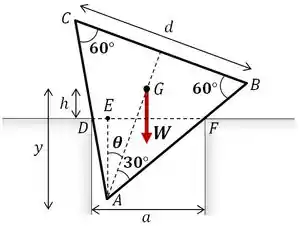
Onde a distância entre o ponto e o centro de gravidade é:
Logo, é dado por:
Passo 2
Podemos tirar ainda outras informações do diagrama de corpo livre. Para descobrirmos a distância do centro de massa (ponto de aplicação de ) até o datum, vamos começar analisando o triângulo formado pelos pontos , e , onde o ângulo entre e pode ser obtido por:
Fazendo o mesmo para o triângulo formado pelos pontos , e , podemos obter o ângulo entre as retas e :
Passo 3
Ainda para esse triângulo , agora que temos todos os seus ângulos internos, podemos usar a lei dos senos para determinar o comprimento da reta e, posteriormente, utilizá-la para determinar . Começando pela lei dos senos no triângulo :
E, finalmente, analisando o triângulo temos que é dado por:
Substituindo por , temos:
Analisando novamente o diagrama de corpo livre, podemos concluir que:
Passo 4
Até aqui só geometria né galera? Essa parte é desgastante, mas é importante para o nosso próximo passo, determinar a equação da energia potencial do sistema. Como nós temos atuando somente o peso do bloco triangular, a energia potencial nesse caso é:
Passo 5
Agora que nós determinamos a equação da energia potencial do sistema, para analisar o equilíbrio do corpo, podemos simplesmente fazer a derivada de em relação a e o resultado deve ser zero. Ou seja:
Daqui já temos que , pois . Continuando resolvendo a equação, o segundo caso é quando:
É isso, galera. Até que foi de boa né?
Partiu pra próxima!
![]()