Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 88
Os blocos e pesam e , respectivamente. Usando os coeficientes de atrito estático indicados, determine o maior peso do bloco sem causar movimento.
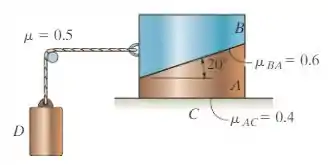
Passo 1
Galerinha, essa questão vamos analisar em 2 passos. O primeiro deles vai ser analisar e como um bloco só, assumindo que não escorrega. Para um sistema em equilíbrio, o somatório das forças tanto em , quanto em é igual a zero.
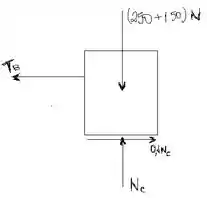
Assim, assumindo a direção para cima como positiva, temos:
Para o eixo , adotando a direção para direita como positiva, temos:
Passo 2
O segundo passo é analisar o bloco isoladamente. Para um sistema em equilíbrio, o somatório das forças tanto em , quanto em é igual a zero.
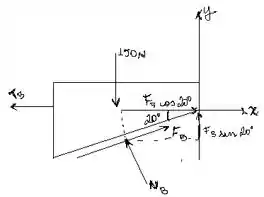
Assim, assumindo a direção para cima como positiva, temos:
Para o eixo , adotando a direção para direita como positiva, temos:
Estamos com um sistema de duas equações e duas incógnitas nas nossas mãos. Isso é mole mole de resolver!
Vamos isolar o na segunda equação:
Vamos substituir esse valor na primeira equação:
Passo 3
Como , ocorre o deslizamento entre e . Portanto, a premissa não foi certa. Como o bloco desliza em , .
Para um sistema em equilíbrio, o somatório das forças tanto em , quanto em é igual a zero.
Assim, assumindo a direção para cima como positiva, temos:
Para o eixo , adotando a direção para direita como positiva, temos:
Passo 4
Para calcular o peso, vamos fazer uso da seguinte expressão:
onde , ,
Resposta
O maior peso do bloco é: