Os blocos e têm uma massa de 100 e , respectivamente. Se os coeficientes de atrito estático entre e e entre e é , e entre as cordas e os pinos e é , determine a menor força necessária para causar movimento do bloco se .

Passo 1
Vamos desenhar o diagrama de corpo livre dessa situação para entendermos a situação da nossa questão!
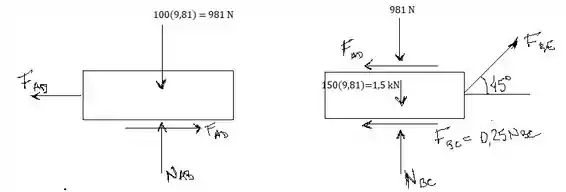
Vamos assumir inicialmente que não há escorregamento entre e .
Passo 2
Vamos começar a resolver essa questão pelo atrito na corda! Quando a corda passa pelo apoio , temos que e vamos assumir que . Então, aplicando a equação para o atrito entre corda e o apoio, temos:
Passo 3
Vamos agora para a análise do equilíbrio. No bloco , para uma situação em equilíbrio, o somatório das forças em e deve ser igual a zero. Assim, assumindo a direção para cima como positiva, temos:
Agora, assumindo a direção para direita como positiva, temos:
Temos aqui duas equações com duas incógnitas! Resolvendo esse sisteminha de equações para encontrar os valores de e .
Passo 4
Quando a corda passa pelo apoio , temos que e vamos assumir que . Então, aplicando a equação para o atrito entre corda e o apoio, temos:
Passo 5
Como se move para a direita, temos:
Aplicando na fórmula do atrito entre a corda e o apoio:
Resposta
A menor força necessária para movimentar o bloco é: