Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 150
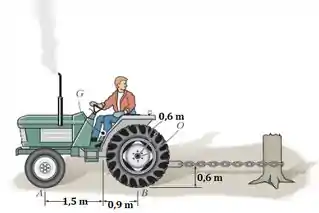
O trato puxa o toco de árvore fixo. Se o coeficiente de atrito estático entre as rodas traseiras e o solo e determine se as rodas traseiras desliam ou se as rodas dianteiras saem do solo enquanto fornece torque para as rodas traseiras. Qual é o torque necessário para causar esse movimento? As rodas da frente estão livres para girar. O trator pesa e tem um centro de gravidade em .
Passo 1
De início, vamos dar uma olhada no diagrama de corpo livre do trator para entendermos as forças que estão atuando.
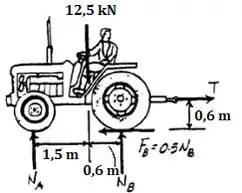
Para essa situação, vamos assumir que as rodas traseiras do tratos deslizam.
Passo 2
Quando nós temos um sistema em equilíbrio, o somatório das forças que atuam nesse sistema, em todos os eixos de referência ( é igual a zero. Vamos aplicar esse princípio na nossa questão! Adotando como direções positivas para cima e para direita, temos o seguinte:
Passo 3
O somatório dos momentos em relação a um ponto, para o sistema em equilíbrio, deve ser igual a zero. Vamos calcular o momento em relação ao ponto e, assumindo como sentido positivo o anti-horário, temos:
Com essa última equação encontrada formamos um sistema de três equações com três incógnitas. Precisamos resolvê-lo para encontrarmos os valores de , e !
Assim, temos:
Passo 4
Encontramos um valor para , o que indica que as rodas dianteiras não levantam. Logo, as rodas traseiras escorregam. Além disso, temos que .
Vamos dar uma olhada agora no diagrama de corpo livre da roda traseira:
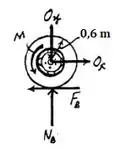
Sabemos que o somatório dos momentos em relação a um ponto, para o sistema em equilíbrio, deve ser igual a zero. Vamos calcular o momento em relação ao ponto e, assumindo como sentido positivo o anti-horário, temos:
Resposta
O torque que precisa ser aplicado pelo motor às rodas traseiras é igual a: