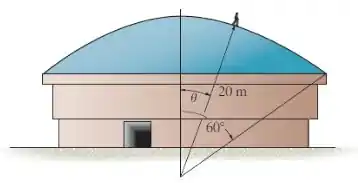
Um reparador de telhados, com uma massa de , caminha lentamente em uma posição ereta ao longo da superfície de um domo que tem um raio de curvatura de . Se o coeficiente de atrito estático entre seus sapatos e o domo é , determine o ângulo em que ele começa a se mover.
Passo 1
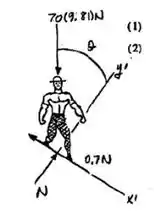
De início, vamos dar uma olhada no diagrama de corpo livre do homem que está trabalhando no topo do domo para entendermos as forças que estão atuando.
Passo 2
Quando nós temos um sistema em equilíbrio, o somatório das forças que atuam nesse sistema, em todos os eixos de referência ( é igual a zero. Queremos achar o ângulo em que ele começa a escorregar. Vamos aplicar esse princípio na nossa questão! Adotando como direções positivas para cima e para direita, temos o seguinte:
Passo 3
Para encontrarmos o valor de ângulo, vamos substituir o valor de na segunda equação encontrada no passo anterior. Assim, temos:
Passo 4
Tendo em mãos o valor do ângulo, podemos agora calcular o valor de . Logo,
Resposta
O ângulo em que ele começa a se mover é igual a: