Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.8 - Ex. 98
O foguete apresentado é projetado para testar o funcionamento de um novo sistema de orientação. Quando ele atinge uma determinada altitude fora da influência efetiva da atmosfera terrestre, sua massa terá diminuída para , e sua trajetória e é de em relação à vertical. O combustível do foguete está sendo consumido na taxa de com uma velocidade de exaustão de em relação ao bocal. A aceleração gravitacional é na sua altitude. Calcule as componentes e da aceleração do foguete.
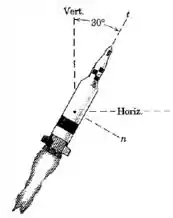
Passo 1
Vamos começar pensando nas forças que atuam sobre o foguete. A primeira, e mais simples, é a força peso, que age na direção vertical, e a segunda é a força de tração gerada pela queima de combustível, que age na direção do movimento:
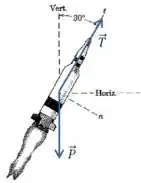
Agora precisamos calcular os módulos de cada uma dessas forças:
Lembrando que é a taxa com que a massa de combustível é queimada, e é a velocidade de exaustão em relação ao bocal.
Passo 2
Se queremos encontrar as componentes e da aceleração precisamos usar as seguintes fórmulas:
Então vamos projetar as duas forças em cada uma das direções, é importante olhar para o desenho que fizemos no passo para entender essas contas. Começando pela :
E agora a direção :
Passo 3
Agora vamos substituir nas equação que mencionamos antes:
E a outra componente é:
Resposta
As componentes são e .