Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 66
O carro se apoia em quatro balanças e, nessa posição, as leituras das rodas dianteiras e traseiras são idicadas por e . Quando as rodas traseiras são elevadas a uma altura de acima das balanças dianteiras, as novas leituras das rodas dianteiras também são registradas. Use esses dados para calcular a localização e do centro de gravidade do carro. Cada um dos pneus tem um diâmetro de .
Passo 1
Fala ai galerinha bonita, tudo beleza?!
O problema pede que encontremos o centro de gravidade do carro. Então vamos analisar um pouco quando o carro está nivelado.
Bom, se a gente somar a reação das rodas a gente encontra o peso do carro, então:
E só pra gente já ficar sabendo o raio da roda é a metade do diâmetro então:
A gente pode usar o momento para ver se a gente consegue encontrar , então vamos usar a equação de equilíbrio do momento, vamos fazer isso tendo como eixo de rotação o ponto :
Logo:
Passo 2
Belezinha, agora a gente vai analisar quando o carro estiver inclinado, vamos fazer um diagraminha de forças:
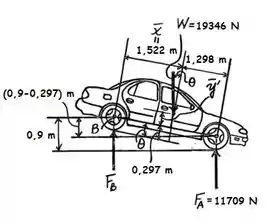
Então já vamos começão olhando só a inclinação pra usar um pouco de trigonometria pra facilitar depois, a gente consegue perceber que:
A gente usa a função inversa do seno na calculadora e encontra:
Passo 3
E denovo a gente usa a equação de equilíbrio pro momento no ponto :
Calculando isso a gente vai encontrar:
Então o centroide em é: