Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 23

23. A boia cilíndrica flutua em água salgada (massa específica de 1030   k g / m 3 ) e possui uma massa de 800   k g , com um centro de massa baixo para mantê-la estável na posição vertical. Determine a frequência f n de oscilação vertical da boia. Suponha que o nível da água permanece sem perturbação na vizinhança da boia.

Passo 1

Bom, primeiro a gente vai montar o diagrama de corpo livre pra boia:

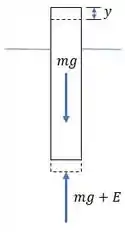
E o que é esse " E " no diagrama? Ele é o Empuxo que agr na boia q flutua e sua fórmula é:

E = μ l í q ⋅ V i ⋅ g

Onde μ l í q é a massa específica do liquido, V i é o volume imerso e g a gravidade local.

E como descobriremos o valor do volume imerso? Como a boia é cilindríca, vamos usar a fórmula da base vezes a altura, onde a altura será o valor de y :

V i = π r 2 y

Onde r é o raio da deção transversal. Como o diâmetro é 0,6   m , o reaio será 0,3   m .

O valor do Empuxo E será:

E = ( 1030 k g / m 3 ) ( π 0,3 2 y   m 3 ) ( 9,81 m / s 2 )

E = 2856,92 y   N

Passo 2

Agora faremos o somatório de forças no eixo y :

∑ F y = m y ¨

A soma é diferente de zero, pois está flutuando, ou seja, há oscilação.

m g - ( m g + E ) = m y ¨

Rearranjando a expressão:

y ¨ + E m = 0

y ¨ + 2856,92   N 800   k g y = 0

Sabemos que a equação genérica para um movimento harmônico:

y ¨ + k m y = 0

Portanto:

k m = 2856,92   N 800   k g

E sabemos também que:

ω n = k m

Substituindo os valores para encontrar ω n :

ω n = 2856,92   N 800   k g

ω n = 3,57

∴ ω n = 1,89   r a d / s

Passo 3

Agora, vamos calcular a frequência pela fórmula:

f n = ω n 2 π

f n = 1,89   r a d / s 2 π

∴ f n = 0,301   H z

Resposta

A frequência de oscilação da boia será:

f n = 0,301   H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

138. Represente graficamente a resposta x do corpo de 20k g ao longo do intervalo de tempo 0 ≤ t ≤ 1 segundo. Determine os valores máximo e mínimo de x e seus respectivos instantes de tempo. As condiç
141. Na figura são apresentados os elementos de um medidor de deslocamentos usado para estudar o movimento y b = b ⋅ s e n ( ω t ) da base. O movimento da massa em relação à carcaça é registrado no ci
137. Uma máquina de 200k g se apoia sobre quatro suportes no chão, cada um dos quais possui uma constante de mola efetiva k = 250k N / m e um coeficiente de amortecimento viscoso efetivo c = 1000 N ⋅
143. Determine e represente graficamente a resposta x = f ( t ) para o oscilador linear não amortecido, submetido à força F que varia linearmente com o tempo, durante os primeiros 3 / 4 de segundo, co
139. A massa de um sistema criticamente amortecido, que possui uma frequência natural ω n = 4r a d / s , é liberada a partir do repouso com um deslocamento inicial x 0 . Determine o tempo t necessário