Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 143

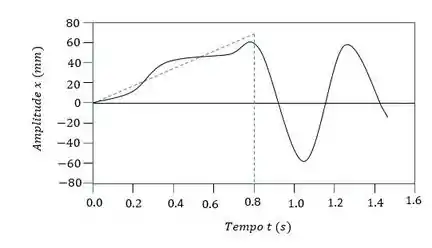
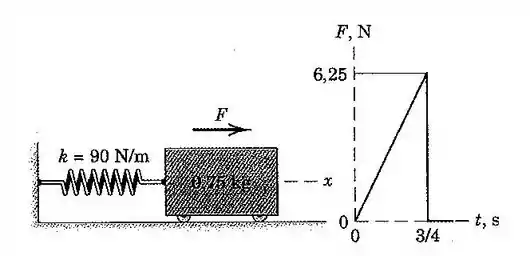
143. Determine e represente graficamente a resposta x = f ( t ) para o oscilador linear não amortecido, submetido à força F que varia linearmente com o tempo, durante os primeiros 3 / 4 de segundo, conforme indicado. A massa está inicialmente em repouso, com x = 0   no instante de tempo   t = 0 .

Passo 1

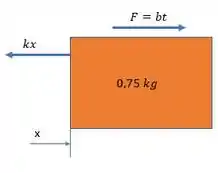
Bom, primeiro vamos montar o diagrama de corpo livre do bloco:

Passo 2

Agora, vamos fazer o somatório de forças no eixo x :

∑ F x = m x ¨

b t - k x = m x ¨

x ¨ + k m x = b t m     ( I )

O fator b nós podemos tirar do gráfico como igual à:

b = F t = 6,25   N 3 / 4 s

b = 8,33   N / s

Passo 3

A solução da nossa equação ( I ) será:

x = x c + x p

Onde x c será:

x c = C 1 ⋅ s e n ω n t + C 2 ⋅ c o s ω n t

E x p será:

x p = C 3 t

Só que C 3 é dado por:

C 3 = b k

x = C 1 ⋅ s e n ω n t + C 2 ⋅ c o s ω n t + b t k

Passo 4

Em seguida, vamos derivar a equação de x em relação ao tempo para encontrar x ˙ :

d d t C 1 ⋅ s e n ω n t = C 1 ω n ⋅ c o s ⁡ ( ω n t )

d d t C 2 ⋅ c o s ω n t = - C 2 ω n ⋅ s e n ⁡ ( ω n t )

d d t b t k = b k

x ˙ = C 1 ω n ⋅ cos ⁡ ω n t - C 2 ω n ⋅ sen ⁡ ω n t + b k

Como o bloco partiu do repouso, x ˙ = 0 e t = 0 :

0 = C 1 ω n ⋅ cos ⁡ 0 - C 2 ω n ⋅ sen ⁡ 0 + b k

C 1 ω n = - b k

C 1 = - b k ω n

E disso concluímos que:

C 2 = 0

Passo 5

Rearranjando x , nós temos que:

x = - b k ω n ⋅ s e n ω n t + b t k

x = b k t - 1 ω n ⋅ s e n ω n t

E depois calculamos ω n pela fórmula:

ω n = k m

Onde k é a constante elástica da mola e m a massa

ω n = 90   N / m 0,75   k g

ω n = 10,95   r a d / s

Para b / k , temos que:

b k = 8,33   N / s 90   N / m = 0,0926   m / s

Passo 6

Agora vamos substituir todos os valores encontrados anteriormente na equação de x :

x = 0,0926   m / s t - 1 10,95   r a d / s ⋅ s e n 10,95 t

x = 0,0926 t - 0,0913 ⋅ s e n 10,95 t m

Isto, valendo é claro, para os primeiros 3 / 4   s .

Resposta

A equação de movimento para os primeiros 3 / 4 s será:

x = 0,0926 t - 0,0913 ⋅ s e n 10,95 t m

E o gráfico será:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sismólogos e geólogos constataram que a Terra vibra com um período de ressonância de 54m i n e um fator Q de cerca de 400 . Após um grande terremoto, a Terra continua vibrando por até 2 meses. (a) Det
Um pêndulo, em seu laboratório de física, tem um comprimento de 75c m e uma bolinha de 15g de massa. Para iniciar o balanço da bolinha, você coloca um ventilador próximo à ela, soprando uma corrente h
Para o cilindro do Prob. 8/8, determine o deslocamento vertical x, medido para baixo no sentido positivo em milímetros, a partir da posição de equilibro, em termos do tempo t, em segundos, medido a pa
Na posição de equilibro, o cilindro de 30 kg provoca uma deflexão estática de 50 mm na mola helicoidal. Se o cilindro é abaixo um adicional de 25 mm e liberado a partir do repouso, calcule a frequênci
Para o sistema do problema 8/3, determine a posição x como uma função do tempo se a massa é liberada no instante de tempo t = 0 a partir de uma posição 50m m à direita da posição de equilíbrio com uma