Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 141

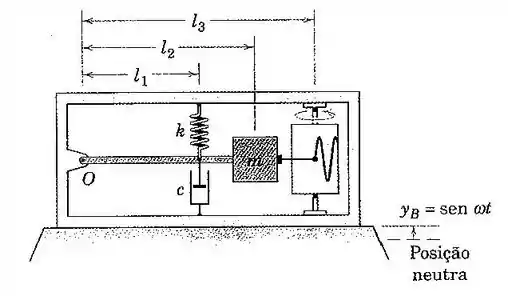
141. Na figura são apresentados os elementos de um medidor de deslocamentos usado para estudar o movimento y b = b ⋅ s e n ( ω t ) da base. O movimento da massa em relação à carcaça é registrado no cilindro giratório. Se l 1 = 360   m m , l 2 = 480   m m , l 3 = 600   m m , m = 0,9   k g , c = 1,4   N ⋅ s / m , e ω = 10   r a d / s , determine a faixa para a constante de mola k por meio da qual a amplitude do deslocamento relativo registrado é inferior a 1,5 b . Assume-se que a razão ω / ω n deve permanecer maior que a unidade.

Passo 1

Primeiro, vamos montar o diagrama corpo livre para nosso medidor:

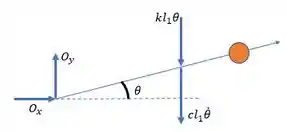
Passo 2

Agora, pela equação:

∑ M O = H ˙ O r + ρ × m a 0

Temos que para pequenos θ , H ˙ O r = m l 2 2 θ ¨ e ρ × m a 0 = k l 2 y ¨ b . (Caso tenha dúvidas, faça a análise dimensional):

- k l 1 2 θ - c l 1 2 θ ˙ = m l 2 2 θ ¨ + k l 2 y ¨ b

Rearranjando a equação:

θ ¨ + c l 1 2 m l 2 2 θ ˙ + k l 1 2 m l 2 2 θ = b l 2 ω 2 ⋅ s e n ( ω t )

Passo 3

Para uma amplitude estável H , temos que:

H = M b ω ω n 2 1 l 2

Onde M é o fator de amplificação

A amplitude do medidor A é dada por:

A = l 3 H = M b ω ω n 2 l 3 l 2

Passo 4

Agora, com o auxílio de um programa, é só calcular para quais valores de k será satisfeita a relação A ≤ 1,5 b .

Observe que:

ω n = l 1 l 2 k m

Onde k é a constante elástica e m a massa.

2 ζ ω n = c l 1 2 m l 2 2

Onde c é o coeficiente de amortecimento e ζ é o fator de amortecimento:

ζ = c l 1 2 l 2 1 k m

ζ 2 = c 2 l 1 2 4 l 2 2 1 k m

4 l 2 2 k m ζ 2 = c 2 l 1 2

l 2 2 = c 2 l 1 2 4 k m ζ 2

l 2 = c 2 l 1 2 4 k m ζ 2

Desse modo, encontramos a amplitude A em função de k , para verificar no computador:

A = l 3 H = M b ω ω n 2 ⋅ l 3 c 2 l 1 2 4 k m ζ 2

E fazendo o cálculo por meio de computação gráfica, obtemos que:

0 < k < 27,63   N / m

Resposta

Os valores de k para que a amplitude seja menor que 1,5 b irão satisfazer a seguinte desigualdade:

0 < k < 27,63   N / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois sistemas massa-mola amortecidos possuem constante elástica e tempo de decaimento idênticos. Porém, a massa m A do sistema A é o dobro da massa m B do sistema B. Como suas constantes de amortecime
Dois sistemas de pêndulos amortecidos forçados possuem massas, forças externas e constantes de amortecimento idênticas. Porém, o comprimento do sistema A é quatro vezes o comprimento do sistema B. Ass
Dois sistemas massa-mola amortecidos forçados oscilando possuem forças externas idênticas assim como constantes de elasticidade e de amortecimento. Porém, a massa m A do sistema A é quatro vezes a mas
Para uma criança em um balanço, a amplitude cai em um fator de 1 e em cerca de oito períodos, se nenhuma energia mecânica adicional for fornecida ao sistema. Estime o fator Q para este sistema.
Mostre que a razão entre as amplitudes de duas oscilações sucessivas é constante para um oscilador linearmente amortecido.