Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 137

137. Uma máquina de 200   k g se apoia sobre quatro suportes no chão, cada um dos quais possui uma constante de mola efetiva k = 250   k N / m e um coeficiente de amortecimento viscoso efetivo c = 1000 N ⋅ s / m . Sabe-se que o chão vibra verticalmente com uma frequência de 24   H z . Qual será o efeito sobre a amplitude de oscilação absoluta da máquina se os suportes forem substituídos por outros novos, que possuem a mesma constante de mola efetiva, porém o dobro do coeficiente de amortecimento efetivo?

Passo 1

Primeiro, vamos montar o diagrama de corpo livre da máquina:

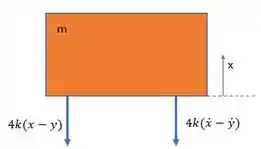
O que a gente pode tirar desse diagrama?

Bom, primeiro as forças estão multiplicadas por 4 porque existem 4 molas.

Já a força k ( x - y ) corresponde à força elástica e a força k ( x ˙ - y ˙ ) corresponde à força de amortecimento.

Fazendo agora o somatório de forças na direção x :

∑ F x = m x ¨

- 4 k x - y - 4 k x ˙ - y ˙ = m x ¨

- 4 k x + 4 k y - 4 k x ˙ + 4 k y ˙ = m x ¨

m x ¨ + 4 k x + 4 k x ˙ = 4 k y + 4 k y ˙

Nós definiremos o movimento do chão como sendo:

y = y 0 ⋅ s e n ( ω t )

y ˙ = y 0 ω ⋅ c o s ( ω t )

Substituindo na equação ali de cima:

m x ¨ + 4 k x + 4 k x ˙ = 4 k y 0 ⋅ s e n ω t + 4 k y 0 ω ⋅ c o s ( ω t )

Passo 2

Agora, vamos calcular a frequência de ressonância ω n , lembrando que devemos multiplicar o k por 4 por ser 4 molas:

ω n = 4 k m = 4 ⋅ 250000   N / m 200   k g

ω n ≅ 70,71   r a d / s

Passo 3

E em seguida, calcularemos o fator de amortecimento ζ :

ζ = 4 c 2 m ω n

Onde é c o amortecimento viscoso efetivo, m a massa da máquina e ω n a frequência de ressonância.

ζ = 4 ⋅ 1000 N ⋅ s / m 2 ( 200   k g ) ( 70,71 r a d / s )

ζ = 0,1414

Passo 4

Assumindo que x p = X s e n ( ω t - α ) , obteremos assim a seguinte relação, que é derivada da expressão para amplitude em regime permanente:

X = F 0 k M

X = F 0 k ⋅ 1 1 - ω ω n 2 2 + 2 ζ ω ω n 2

X = 1 + 2 ζ ω ω n 2 y 0 1 - ω ω n 2 2 + 2 ζ ω ω n 2

Onde X é a amplitude:

X = 1 + 2 ( 0,1414 ) ω ( 70,71 r a d / s ) 2 y 0 1 - ω ( 70,71 r a d / s ) 2 2 + 2 ( 0,1414 ) ω ( 70,71 r a d / s ) 2

Isso nos resulta em:

X = 0,325   y 0

Passo 5

E desse modo, se dobrarmos o amortecimento, obteremos uma nova amplitude X ' igual a:

X ' = 0,418   y 0

Passo 6

Finalmente, vamos ver o quanto aumentará a amplitude se for dobrado o amortecimento:

0,325   y 0 100   % = 0,418   y 0 z   %

z   % = 100   % ⋅ 0,418   y 0 0,325   y 0

z = 128,61   %

O aumento foi a subtração desse z   com 100 % , portanto de 28,61   % .

Resposta

Se duplicado o coeficiente de amortecimento, a amplitude será aumentada em:

28,6   %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um oscilador linearmente amortecido possui um fator Q igual a 20 . (a) Qual é a fração de redução da energia, em cada ciclo? (b) Use a equação para determinar a diferença percentual entre ω ' e ω 0 .
Um oscilador tem um período de 3,00s . Sua amplitude diminui 5,00 por cento em cada ciclo. (a) De quanto diminui sua energia mecânica em cada ciclo? (b) Qual é a constante de tempo τ ? (c) Qual é o fa
Um corpo de 2,00k g oscila preso a uma mola, com uma amplitude inicial de 3,00c m . A constante de força da mola é 400N / m . Determine (a) o período e (b) a energia total inicial. (c) Se a energia di
Um sistema massa-mola linearmente amortecido oscila a 200H z . A constante de tempo do sistema é 2,0s . Em t = 0 , a amplitude de oscilação é 6,0c m e a energia do sistema oscilante é 60J . (a) Quais
Você deve monitorar a viscosidade de óleos em uma indústria, e determina a viscosidade de um óleo usando o seguinte método. A viscosidade de um fluido pode ser medida determinando-se o tempo de decaim