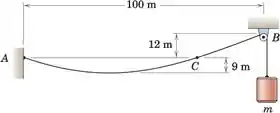
Um cabo pesando 25 newtons por metro de comprimento é suspenso do ponto A e passa sobre a pequena polia em B. Calcule a massa m do cilindro acoplado que produzirá o afundamento de 9 m. Determine também a distância horizontal de A a C. Por causa da pequena razão de curvatura para amplitude, use a aproximação de um cabo parabólico.
Passo 1
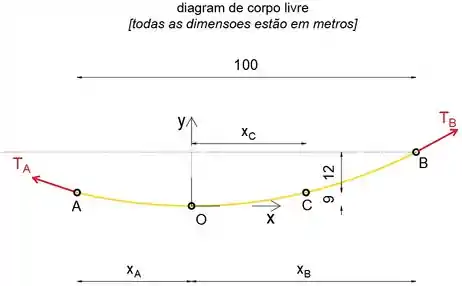
Vamos desenhar o diagrama de corpo livre do cabo.
Podemos ver que as coordenadas dos pontos A e B são:
Também podemos ver que a distância horizontal entre A e B é:
E o peso do cabo por unidade de comprimento é:
Observe que os pontos A e C estão na mesma altura, portanto as distâncias horizontais xA e xc são iguais.
Sabendo disso, podemos escrever a distância horizontal entre os pontos A e C como:
Passo 2
Uma vez que o cabo é aproximado como parabólico, sua função é:
A partir daqui, podemos expressar T0 como:
Finalmente, substitua w por seu valor para obter:
Podemos determinar a componente vertical da tensão no cabo (T0) colocando as coordenadas dos pontos A e B na expressão (3).
Ponto A:
Passo 3
A partir daqui, podemos expressar xA como:
Ponto B:
A partir daqui, podemos expressar xB como:
A seguir, podemos substituir xa e xb na equação (1) pelas expressões (A) e (B)
A partir daqui, podemos expressar como:
Quadrado ambos os lados da equação para calcular o valor do componente horizontal da tensão
Colocando o valor de T0 na expressão (A), podemos determinar xA.
Finalmente, substitua xA por seu valor na equação (2)
Passo 4
Observe que, para determinar a tensão no cabo no ponto B, precisaremos determinar a distância xB. Podemos fazer isso colocando o valor de xA na equação (1) ou T0 na equação (B).
Como sabemos o peso do cabo por metro, coordenada x do ponto B e o componente horizontal da tensão, podemos calcular a tensão no ponto B.
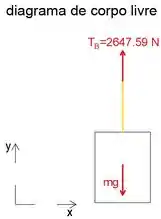
Finalmente, iremos isolar e desenhar o diagrama de corpo livre do cilindro.
Observe que a tensão no cabo preso ao cilindro é igual à tensão no cabo no ponto B por causa da polia.
Passo 5
Equacionando a soma das forças na direção y a zero, podemos determinar a massa m