Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 91
O carro de está viajando a sobre a porção reta da estrada, e então sua velocidade é reduzida uniformemente de para , posição em que este atinge o repouso. Calcule o módulo da força de atrito total exercida pela estrada sobre o carro (a) pouco antes de este passar o ponto , (b) pouco depois que este passa o ponto , e (c) pouco antes deste parar no ponto .
Passo 1
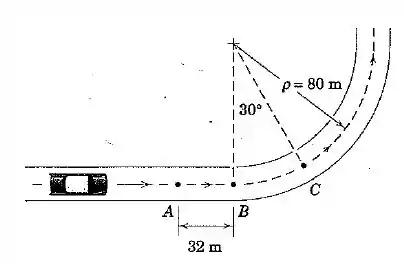
Vamos começar calculando a distância que o carro percorre entre os pontos e :
Onde a fração serve para converter os para radianos::
Com isso a gente pode descobrir qual era a aceleração tangencial que faz o carro atingir o respouso quando chega no ponto :
Beleza, isso já vai nos ajudar a responder as outras perguntas.
Passo 2
(a) Queremos saber a força de atrito total exercida pela estrada sobre o carro pouco antes de passar pelo ponto .
Bom, nesse caso a única força de atrito é a que produz a desaceleração que acabamos de calcular, então pela segunda lei de Newton:
E o sinal negativo aparece porque adotamos o sentido como positivo.
Passo 3
(b) Logo depois que o carro passa pelo ponto , passa a existir uma “nova” força de atrito que mantém o carro na trajetória circular, ou seja, o atrito cumpre o papel de força centrípeta.
E podemos descobrir a velocidade em fazendo o seguinte:
E então:
Lembre-se, a outra componente da força de atrito continua existindo, e é perpendicular a essa, e então a força de atrito total é:
Passo 4
(c) E o que muda entre os pontos e ? Simples: a velocidade do carro terá diminuído praticamente até o zero, de forma que a força centrípeta (que é mantida exclusivamente por uma das componentes do atrito) é:
Mas a outra componente continua existindo, já que o carro não está totalmente parado ainda:
E então voltamos ao que tínhamos na letra (a):
Resposta
(a)
(b)
(c)