Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 123

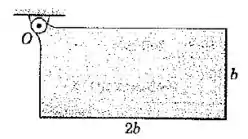
A placa retangular uniforme é liberada a partir do repouso na posição indicada. Determine a velocidade angular máxima ω durante o movimento que se segue. O atrito na articulação é desprezível.

Passo 1

Vamos começar calculando o momento de inércia do sistema em relação ao ponto O . Para isso vamos precisar do teorema dos eixos paralelos:

I O = I c m + m d 2

O momento de inércia em relação ao centro de massa pode ser consultado em uma tabela:

I c m = 1 12 m b 2 + 2 b 2

E a distância d pode ser calculada com o teorema de pitágora:

d 2 = 2 b 2 2 + b 2 2 = 5 4 b 2

Então:

I O = 1 12 m b 2 + 2 b 2 + 5 4 m b 2

I O = 5 3 m b 2

Com esse resultado, podemos escrever uma expressão para a energia cinética da placa conforme ela adquire uma velocidade angular ω em torno de O :

T = 1 2 I O ω 2 = 1 2 5 3 m b 2 ω 2

T = 5 6 m b 2 ω 2

Passo 2

Conforme o centro de massa da placa cai por uma altura h , a variação na energia potencial gravitacional é dada por:

Δ U = - m g h

Então, pela lei de conseração de energia (sabendo que T 0 = 0 ):

Δ T + Δ U = 0

T = - Δ U

T = m g h

Então:

5 6 m b 2 ω 2 = m g h

5 6 b 2 ω 2 = g h

A velocidade angular máxima vai acontecer quando h também for máxima. Vamos isolar ω nessa equação:

ω = 6 g h 5 b 2

Passo 3

Agora vamos procurar uma expressão para altura h pela qual o centro de massa cai durante o movimento:

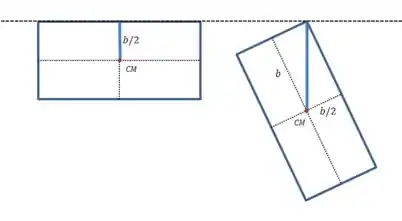
E a diferença entre essas duas alturas é:

h = b 2 2 + b 2 - b 2

h = 5 b 2 - b 2 = 5 - 1 b 2

Então:

ω = 6 g 5 - 1 b 2 5 b 2 = 6 g 5 - 1 10 b

Agora vamos substituir os valores numéricos:

ω = 6 5 - 1 ( 10 ) g b

ω = 0,861   g b

Resposta

A velocidade angular máxima será ω = 0,861   g b .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o canto A da placa de 60 kg é submetido a uma força vertical P = 500 N, e a placa é liberada do repouso quando θ = 0 ° , determine a velocidade angular da placa quando θ = 45 ° .
Se o balde de 25 kg é solto do repouso, determine sua velocidade após haver caído a uma distância de 3 m. O sarilho A pode ser considerado como um cilindro de 15 kg, enquanto seus raios são barras fin
A escada de 15 kg está colocada contra a parede em um ângulo de θ = 45 ° , como mostrado. Se ela é liberada do repouso, determine sua velocidade angular no instante imediatamente anterior a θ = 0 ° .
Determine a velocidade angular das duas barras de 10 kg quando θ = 9 0 ° , se elas são liberadas do repouso na posição θ = 60 ° . Despreze o atrito.
O bloco de 50 kg é transportado por uma distância curta, usando-se dois rolos cilíndricos, cada um com massa de 17,5 kg. Se uma força horizontal P = 125 N é aplicada ao bloco, determine a velocidade d