Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 121

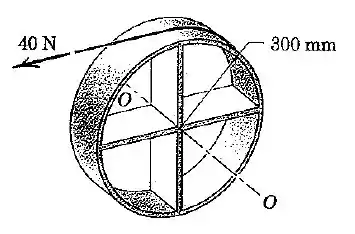
A roda é composta por um aro de 10   k g enrijecido por quatro raios finos, cada um com uma massa de 2   k g . Uma força horizontal de 40   N é aplicada à roda inicialmente em repouso. Calcule a velocidade angular da roda após o seu centro ter se deslocado 3   m . O atrito é suficientepara evitar o deslizamento.

Passo 1

Vamos começar escrevendo expressões para as energias cinéticas do aro e dos raios finos.

Δ T a r o = 1 2 m a v 2 + 1 2 I ω 2

Δ T a r o = 1 2 m a v 2 + 1 2 m a r 2 ω 2

E podemos reescrever v = ω r :

Δ T a r o = m a r 2 ω 2

Agora vamos olhar par os raios. Podemos tratá-los como dois pares, cada um com comprimento 2 r :

Δ T r a i o s = 2 1 2 m r v 2 + 1 2 I ω 2

E nesse caso I será o momento de inércia de uma haste de comprimento 2 r :

Δ T r a i o s = 2 1 2 m r v 2 + 1 2 1 12 m r 2 r 2 ω 2

Mais uma vez, vamos reescrever v = ω r :

Δ T r a i o s = m r r 2 ω 2 + 1 3 m r r 2 ω 2 = 4 3 m r r 2 ω 2

Então a energia cinética total do sistema é:

Δ T = Δ T a r o + Δ T r a i o s

Δ T = m a r 2 ω 2 + 4 3 m r r 2 ω 2

Δ T = 10 0,3 2 ω 2 + 4 3 2 2 0,3 2 ω 2 = 1,38   ω 2

Passo 2

Agora vamos lembrar da seguinte igualdade:

W = Δ T

Onde W é o trabalho das forças que agem sobre o aro.

Nesse caso, temos uma força de 40   N puxando o arco para a esquerda, e como não há deslizamento, temos uma força de atrito com o mesmo módulo que favorece o movimento na mesma direção.

Juntas, essas forças causam um deslocamento de 3   m , então:

W = 2 40 3 = 240   J

Podemos substituir isso na equação de cima:

240 = 1,38   ω 2

ω = 13,19   r a d / s

Resposta

A velocidade angular será ω = 13,19   r a d / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando uma força P = 150 N é aplicada à alavanca do freio, o cilindro A, de 25 kg, está descendo a uma velocidade de 6 m/s. Determine o número de revoluções que a roda B rotacionará antes que seja par
A montagem consiste de duas barras finas de 7,5 kg e de um disco de 10 kg. Se a mola não está deformada quando θ = 45 ° e a montagem é liberada do repouso nessa posição, determine a velocidade angular
A porta uniforme tem massa de 20 kg e pode ser tratada como uma placa fina, tendo as dimensões mostradas na figura. Se ela está conectada a uma mola torsional em A, que tem rigidez k = 80N . m / r a d
A viga fina, tendo uma massa de 75 kg, é suportada por dois cabos. Se o cabo na extremidade B é cortado, de modo que a viga seja liberada do repouso quando θ = 30 ° , determine a velocidade com que a
A bobina tem uma massa de 100 kg e raio de giração de 400 mm em relação a seu centro de massa O. Se ela é liberada do repouso, determine sua velocidade angular após seu centro O haver descido pelo pla