Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 42

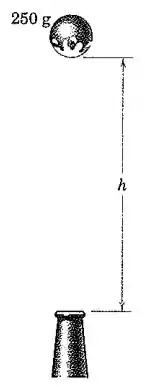
A bola de 250   g é suportada pelo jato vertical de água doce que escoa a partir do bocal com 12   m m de diâmetro a uma velocidade de 10   m / s . Calcule a altura h da bola acima do bocal. Suponha que o escoamento permanece sem modificação e que não há energia perdida na corrente do jato.

Passo 1

A corrente de água sai do bocal com uma velocidade v 0 = 10   m / s , e conservando sua energia mecânica, chega à altura h com velocidade v . Quando toca na bola, a corrente será desviada perpendicularmente, de modo que a velocidade vertical final da corrente é nula. Essa alteração na quantidade de movimento da água “cria” uma força para cima na bola, que equilibra o peso P da bola, assim:

- P = m ' Δ v y

Para calcular a taxa de escoamento m ' , fazemos assim:

m ' = ρ A v 0

m ' = 1000 π 0,012 2 4 10

m ' = 1,13   k g / s

Passo 2

Então, voltamos na equação de equilíbrio da bola:

- P = m ' Δ v y

- m B g = m ' 0 - v

v = m B g m '

v = ( 0,250 ) ( 9,81 ) 1,13

v = 2,17   m / s

Passo 3

Agora, tendo o valor de v na altura h , podemos determinar h pela conservação da energia da água:

Δ T + Δ V g = 0

1 2 m v 2 - 1 2 m v 0 2 + m g h - 0 = 0

h = 1 2 g v 0 2 - v 2

h = 1 2 9,81 10 2 - 2,17 2

h = 4,86   m

Resposta

h = 4,86   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um esquiador pesando 90k g parte do repouso para descer uma encosta com inclinação de 17 ° . Ele desliza 100m encosta abaixo e, a seguir interrompe a impulsão ao longo de 70m de neve nivelada até para
Dois blocos de massas diferentes são conectados por um fio sobre uma polia lisa (Figura 2.B). Se o coeficiente de atrito cinético é µ kµ , qual é o ângulo θ do plano inclinado que permite o movimento
Uma estudante deixa cair uma bexiga cheia de água da cobertura do prédio mais alto na cidade para atingir sua colega de quarto no chão (que é muito rápida). A primeira estudante se esconde, mas ouve o
Um motorista dirigindo um automóvel sobre um declive com 8% de inclinação efetua uma frenagem abrupta e "patina" por uma distância de 30 m antes de colidir com um carro estacionado. Um advogado contra
Uma partícula é liberada do repouso y = 0 e cai sob a influência da gravidade e da resistência do ar. Determine o relacionamento entre v , e a distância de queda y , quando a resistência do ar for igu