Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 165
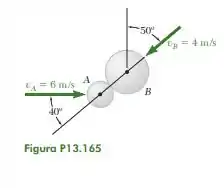
Uma bola A de move-se com velocidade de de intensidade quando é atingida por uma bola B de que tem velocidade de de intensidade. Sabendo que o coeficiente de restituição é 0,8 e desprezando o atrito, determine a velocidade de cada bola após o impacto.
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Primeiro, primeiro vamos lembrar as relações que valem pra esse tipo de problema, que é um caso de impacto oblíquo.
Na direção do eixo de impacto, direção normal, temos as seguintes relações, que e é o coeficiente de restituição:
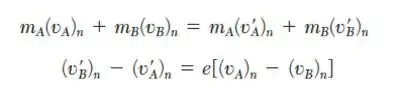
Na direção perpendicular ao eixo de impacto, ou direção tangencial, as velocidades de cada corpo se conservam:
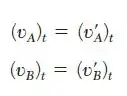
Passo 2
Agora vamos substituir nossos valores nas fórmulas. Na direção tangencial, temos:
Na direção normal:
As duas equações pras componentes normais formam um sistema. Resolvendo, encontramos:
Passo 3
Agora que temos as componentes normais e tangenciais das velocidades finais de A e B, vamos encontrar o valor total das velocidades.