Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 88

A bola A atinge a bola B com uma velocidade inicial v A 1 como mostrado. Se as duas bolas têm a mesma massa e a colisão é perfeitamente elástica, determine o ângulo θ após a colisão. A bola B está originalmente em repouso. Despreze a dimensão de cada bola.

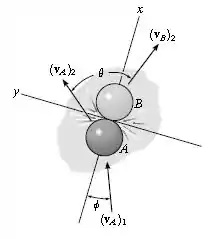
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Antes do impacto temos:

v A x 1 = v A 1 cos ⁡ ϕ

v B x 1 = 0

v A y 1 = v A 1 sin ⁡ ϕ

v B y 1 = 0

Após o impacto, teremos:

v A x 2 = v A 2 cos ⁡ θ 1

v B x 2 = v B 2 cos ⁡ θ 2

v A y 2 = v A 2 sin ⁡ θ 1

v B y 2 = - v B 2 sin ⁡ θ 2

Agora que organizamos nossos dados, vamos aplicar a conservação de quantidade de movimento linear:

m B v B y 1 = m B v B y 2

0 = m - v B 2 sin ⁡ θ 2

θ 2 = 0 °

Em x , temos:

m A v A x 1 + m B v B x 1 = m A v A x 2 + m B v B x 2

m v A 1 cos ⁡ ϕ + 0 = m v A 2 cos ⁡ θ 1 + m v B 2 cos ⁡ θ 2

v A 1 cos ⁡ ϕ = v A 2 cos ⁡ θ 1 + v B 2 cos ⁡ θ 2

Analisando a restituição, temos:

    e = v B x 2 - v A x 2 v A x 1 - v B x 1

Como a colisão é perfeitamente elática, e = 1 :

1 = v B 2 cos ⁡ θ 2 - v A 2 cos ⁡ θ 1 v A 1 cos ⁡ ϕ - 0

v B 2 cos ⁡ θ 2 - v A 2 cos ⁡ θ 1 = v A 1 cos ⁡ ϕ

Agora, vamos substituir as seguintes equações:

v B 2 cos ⁡ θ 2 - v A 2 cos ⁡ θ 1 = v A 1 cos ⁡ ϕ

v A 1 cos ⁡ ϕ = v A 2 cos ⁡ θ 1 + v B 2 cos ⁡ θ 2

Temos:

v B 2 cos ⁡ θ 2 - v A 2 cos ⁡ θ 1 = v A 2 cos ⁡ θ 1 + v B 2 cos ⁡ θ 2

2 v A 2 cos ⁡ θ 1 = 0

θ 1 = 90 °

θ = θ 1 + θ 2

θ = 90 ° + 0 °

θ = 90 °

Resposta

θ = 90 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As duas pequenas esferas, cada uma com massa m , estão rigidamente conectadas por uma haste de massa desprezível. O centro C da haste possui uma velocidade v na direção x , e a haste está girando no s
Três macacos A , B e C , com massas de 10 , 15 e 8k g , respectivamente, estão subindo e descendo a corda suspensa a partir de D . No instante representado, A está descendo a corda com uma aceleração
O sistema de três partículas possui as massas, velocidades e forças externas indicadas nas partículas. Determine r - , r - ˙ , r - ¨ , T , H O e H O ˙ para esse sistema.
Os três vagões de carga estão se deslocando ao longo do trilho horizontal com as velocidades indicadas. Após os impactos ocorrerem, os três vagões se tornam acoplados e se movem com uma velocidade com
O homem de massa m 1 e a mulher de massa m 2 estão em pé sobre extremos opostos da plataforma de massa m 0 que se desloca com atrito desprezível e está inicialmente em repouso com s = 0 . O homem e a