Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 84

Dois discos A e B têm massa de 1   k g e 2,5   k g , respectivamente. Se eles deslizam sobre um plano horizontal liso com as velocidades mostradas, determine suas velocidades logo após o impacto. O coeficiente de restituição entre os discos é e = 0,6 .

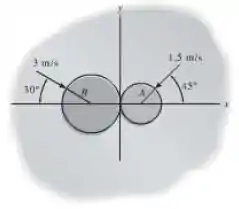
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos aplicar a conservação de quantidade de movimento linear paras os corpos A e B , para analisar as velociadades antes e após o impacto.

Como temos componentes das velocidades em y e x , então vamos analisar para os dois eixos:

→ +     ∑ m 1 v x 1 = ∑ m 2 v x 2

m A v A x + m B v B x = m A v A ' x + m B v B ' x

- 1 1,5 cos ⁡ 45 ° + 2,5 ( 3 ) cos ⁡ 30 ° = 1 v A ' cos ⁡ θ A + 2,5 v B ' cos ⁡ θ B

v A ' cos ⁡ θ A + 2,5 v B ' cos ⁡ θ B = 5,4345

Aplicando o mesmo procedimento de conservação de quantidade de movimento linear para o eixo y , temos:

m A v A y = m A v A ' y

1 ( 1,5 ) sin ⁡ 45 ° = 1 v A ' sin ⁡ θ A

v A ' sin ⁡ θ A = 1,061   m / s

m B v B y = m B v B ' y

2,5 3 sin ⁡ 30 ° = 2,5 v B ' sin ⁡ θ B

v B ' sin ⁡ θ B = 1,5   m / s

Analisando a restituição, temos:

+ ↘     e = v A ' x - v B ' x v B x - v A x

0,6 = v A ' cos ⁡ θ A - v B ' cos ⁡ θ B 3 cos ⁡ 30 ° - ( - 1,5 cos ⁡ 45 ° )

v A ' cos ⁡ θ A - v B ' cos ⁡ θ B = 2,2

Agora, vamos subtrair as seguintes equações:

v A ' cos ⁡ θ A + 2,5 v B ' cos ⁡ θ B = 5,4345

v A ' cos ⁡ θ A - v B ' cos ⁡ θ B = 2,2

Temos:

v A ' cos ⁡ θ A + 2,5 v B ' cos ⁡ θ B - v A ' cos ⁡ θ A - v B ' cos ⁡ θ B = 5,4345 - 2,2

3,5 v B ' cos ⁡ θ B = 3,2345

v B ' cos ⁡ θ B = 0,924

Temos que:

v A ' cos ⁡ θ A - 0,924 = 2,2

v A ' cos ⁡ θ A = 3,124

Passo 2

Agora só precisamos fazer algumas manipulações para conseguir encontrar os nossos resultados:

v A ' sin ⁡ θ A v A ' cos ⁡ θ A = 1,061 3,124

tan ⁡ θ A = 1,061 3,124

θ A = tan - 1 ⁡ 1,061 3,124

θ A = 18,8 °

Logo:

v A ' cos ⁡ 18,8 ° = 3,124

v A ' = 3,3   m / s

Fazendo o mesmo procedimento para B , temos:

v B ' sin ⁡ θ B v B ' cos ⁡ θ B = 1,5 0,924

tan ⁡ θ B = 1,5 0,924

θ B = tan - 1 ⁡ 1,5 0,924

θ B = 58,4 °

E:

v B ' cos ⁡ 58,4 ° = 0,924

v B ' = 1,76   m / s

Resposta

θ A = 18,8 °

v A ' = 3,3   m / s

θ B = 58,4 °

v B ' = 1,76   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A mulher A de 60k g , o capitão B de 90k g , e o marinheiro C de 80k g estão sentados no barco de 150k g , que está deslizando através da água com uma velocidade de 1 nó. Se as três pessoas mudam suas
As três pequenas esferas de aço, cada uma com massa de 2,75k g , estão unidas pelas conexões articuladas de massa desprezível e comprimentos iguais. As esferas são liberadas a partir do repouso nas po
As duas esferas estão rigidamente conectadas à haste de massa desprezível e estão inicialmente em repouso sobre a superfície horizontal lisa. Uma força F é aplicada repentinamente a uma esfera na dire
Na posição não esticada as espiras da mola de 1,5k g estão quase tocando uma na outra, como mostrado na parte (a) da figura. Na posição esticada a força P , proporcional a x , é igual a 900N quando x
O vagão-plataforma de 25t suporta um veículo de 7,5t em uma rampa de 5 ° construída sobre o vagão-plataforma. Se o veículo é liberado a partir do repouso com o vagão-plataforma também em repouso, dete