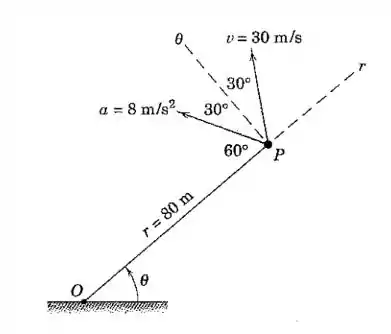
No instante representado, suponha que a partícula , que se move em uma trajetória curva, está a do pólo e tem a velocidade e a aceleração conforme indicado. Determine os valores instantâneos de , , , , as componentes e da aceleração, e o raio de curvatura .

Ok, então vamos lembrar de algumas relações entre essas grandezas. Primeiro a velocidade:

Essas fórmulas são bem intuitivas! A primeira diz que a é a velocidade com que o corpo gira com o ângulo , e a segunda diz que é a taxa em que o raio muda!

Substituindo os valores numéricos:

E as fórmulas para as componentes da aceleração em coordenadas polares são:

Agora vamos substituir os números:

Ótimo, agora só falta calcular o raio de curvatura da trajetória. Aqui é preciso tomar cuidado, porque você pode ter a intuição de fazer o seguinte:

Mas isso não está certo! Essa fórmula vale para a , a aceleração normal à velocidade, e esse não é o caso da linha pontilhada da figura.

Pela mesma lógica, o que nós calculamos não é a aceleração tangencial , porque esta tem que ser paralela à velocidade, e esse não é o caso da linha pontilhada da figura!

Vamos desenhar os vetores que realmente queremos encontrar:

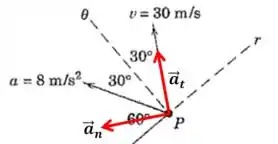
Agora sim, vamos projetar a aceleração nesses vetores vermelhos para encontrar os módulos:

Esse ângulo de que usamos na expressão do é deduzido do fato de que e são perpendiculares, então é só subtrair aqueles dois ângulos de do total de .

Agora sim podemos aplicar aquela fórmula:

Pronto!