Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 29

Se o carro desacelera uniformemente ao longo da estrada curva de 25   m / s em A para 15   m / s em C, determine a aceleração do carro em B.

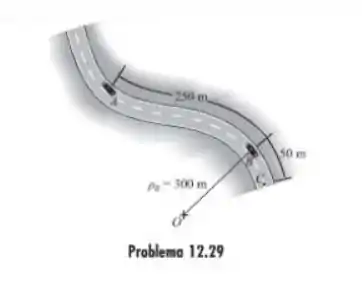
Passo 1

Como estamos trabalhando com uma aceleração constante, podemos utilizar todas as equações da cinemática já discutidas no capítulo! Precisamos descobrir então qual é a aceleração tangencial do carro (a qual é negativa, já que a velocidade diminui), e depois descobrir a sua velocidade no ponto B, para que possamos calcular a componente normal da aceleração!

Passo 2

Começaremos determinando a aceleração tangencial. Para isto, vamos utilizar a relação de velocidade e aceleração em função da posição. Isto é:

v 2 - v 0 2 = 2 a t Δ s

15 2 - 25 2 = 2 a t ⋅ 300

a t = 15 2 - 25 2 600

a t = - 2 3 = - 0,66 67   m / s 2

Passo 3

Agora, temos que descobrir a velocidade do carro no ponto B, após ele percorrer uma distância de Δ s = 2 50   m . Sendo assim,

v 2 - 25 2 = 2 ⋅ - 0,6667 ⋅ 2 50

v = 17,08   m / s

Passo 4

Agora podemos calcular a aceleração do carro. Calculando a sua componente normal antes, temos:

a n = v 2 ρ = 17,08 2 300 = 0,9722   m / s 2

Portanto, calculando a intensidade da aceleração, temos:

a = a n 2 + a t 2

a = 0,9722 2 + ( - 0,66 67 ) 2

a = 1 , 18   m / s 2

Resposta

a = 1 , 18   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um piloto de jato sabe que é capaz de suportar uma aceleração de 9 g antes de perder os sentidos. Ele aponta sua aeronave verticalmente para baixo voando em velocidade Mach3 e pretende arremeter em um
Um palhaço faz malabarismo com quatro bolas simultaneamente. Os alunos utilizam uma gravação em vídeo para determinar que o palhaço leva 0,9s para trocar cada bola entre suas mãos (inclui pegar, trans
Inclua a resistência do ar para os fardos de feno no problema anterior. Um fardo de feno tem massa aproximada de 30k g e área de cerca de 0,2m 2 . Considere a resistência do ar proporcional ao quadrad
Inclua a resistência do ar proporcional ao quadrado da velocidade da bola no problema anterior. Considere o coeficiente de arrasto como sendo c w = 0,5 , o raio da bola igual a 5c m e sua massa 200g .
Um cubo sólido de densidade uniforme e lados com dimensão b se encontra em equilíbrio na parte superior de um cilindro de raio R (Figura 2.C). Os planos dos quatro lados do cubo são paralelos ao eixo