Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 29
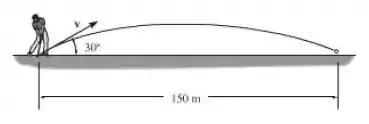
A bola de golfe de é atingida pelo taco e desloca-se ao longo da trajetória mostrada. Determine a força impulsiva média que o taco transmite à bola, se o taco mantém contato com a bola durante .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O diagrama de corpo livre do sistema é dado por:
Para encontrarmos força média, temos que encontrar a velocidade final para aplicar no principio do impulso e quantidade de movimento.
Podemos encontrar essa velocidade a partir da analise do movimento oblíquo.
Considerando o movimento horizontal, temos:
Do movimento vertical, temos:
Passo 2
Aplicando o principio do impulso e quantidade de movimento, temos:
Resposta
Exercícios de Livros Relacionados
O carro com tração nas rodas traseiras possui uma massa de 1600 kg com centro de massa em G . O coeficiente de atrito efetivo entre os pneus e a estrada é de 0.80 . considere o carro e as rodas como u
A barra esbelta uniforme tem uma massa de 30k g e é liberada a partir do repouso na posição próxima da vertical mostrada, onde a mola com rigidez de 150N / m está sem deformação. Calcule a velocidade
Cada um dos blocos quadrados maciços pode tombar girando no sentido horário a partir das posições de repouso mostradas. O suporte em O no caso (a) é uma rótula e no caso (b) é um pequeno rolete. Deter
O pequeno bloco de massa m desliza na ranhura radial lisa do disco, que gira livremente em seu mancal. Se o bloco é ligeiramente deslocado da posição central quando a velocidade angular do disco é ω 0
O anel de raio r com uma abertura está girando em torno de um eixo vertical através do seu centro O com uma velocidade angular constante ω . Utilize um elemento diferencial do anel e desenvolva expres