Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 222
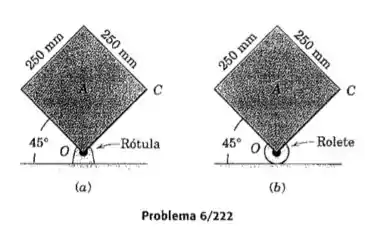
Cada um dos blocos quadrados maciços pode tombar girando no sentido horário a partir das posições de repouso mostradas. O suporte em O no caso (a) é uma rótula e no caso (b) é um pequeno rolete. Determine a velocidade angular de cada bloco quando o lado se torna horizontal pouco antes de atingir a superfície de apoio
Passo 1
Para a letra (a), vamos precisar aplicar a lei de conservação de energia. A única força que atua no sistema é a gravitacional, que corresponde à energia potencial gravitacional, portanto:
A energia cinética inicial é zero pois o bloco parte do repouso, e a final será:
A energia potencial gravitacional será zero no final, pois vamos colocar a altura do centro de massa do bloco no momento final, exatamente no zero da coordenada y, sobrando apenas a energia inicial:
A equação de conservação fica:
Passo 2
Precisamos agora determinar o momento de inercia do bloco em relação ao eixo que passa no ponto O, para isso, vamos usar o teorema dos eixos paralelos:
Onde l é o lado do quadrado e R será a distancia até o ponto O, dado pelo valor de um dos catetos formados entre o vértice do losango e o centro de massa ( a hipotenusa é um dos lados do losango):
E a altura do bloco no momento inicial será:
O último termo da diferença será a metade do valor de um dos lados, que é a posição do centro de massa após o bloco rotacionar, e o primeiro termo, será o valor do cateto que o centro de massa forma com o vértice do losango.
Passo 3
Substituindo os valores na equação de conservação para encontrarmos :
Passo 4
No caso da letra (b), o rolete irá deslizar para a esquerda caso o bloco rotacione para a direita, então a velocidade do centro de massa irá permanecer vertical, dessa forma, podemos escrever a velocidade do centro de massa como a velocidade do ponto O em relação ao centro de massa:
Sendo que:
Ou seja, o ponto O girou em relação ao referencial no centro de massa, e a distancia é a distancia entre o centro de massa e o ponto O (que é o mesmo c q calculamos antes. Ficamos com:
Passo 5
E agora aplicamos novamente a lei de conservação de energia, utilizando as mesmas ideias anteriormente, mas agora, com a energia cinética do movimento do centro de massa:
Perceba que o momento de inercia não será mais em relação ao ponto O, pois já consideramos o seu movimento na energia cinética translacional.
Isolando e cortando as massas (o m que acompanha o 0.016 é metros):