Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 180

A corrente de comprimento L é liberada a partir do repouso sobre o plano inclinado liso com x = 0 . Determine a velocidade v dos elos em termos de x .

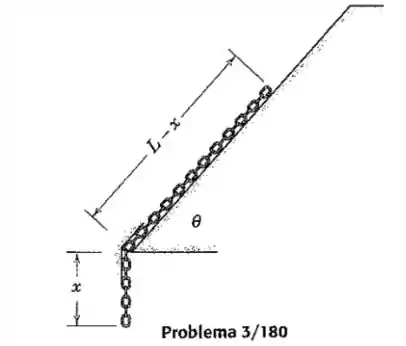
Passo 1

Vamos pensar na energia mecânica da corrente conforme ela desce o plano. Se ela parte do repouso e adquire uma velocidade v , a variação da sua energia cinética é:

Δ T = 1 2 ρ L v 2

Onde ρ é a densidade linear da corrente e L é o seu comprimento.

Mas e a energia potencial gravitacional? Bom, vamos pensar em um trecho de corrente com comprimento x . O essencial aqui é pensar no centro de massa desse trecho, que está na metade desse comprimento x .

Vamos desenhar o efeito do deslocamento do centro de massa desse pedaço na corrente:

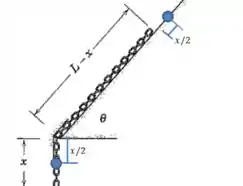
Mas o que importa para a energia potencial gravitacional é o deslocamento no eixo vertical:

Δ h = L - x sen ⁡ θ + x 2 sen ⁡ θ + x 2

E então a variação de energia potencial é:

Δ U = - ρ g x L - x sen ⁡ θ + x 2 sen ⁡ θ + x 2

Passo 2

Agora pela conservação de energia:

Δ T + Δ U = 0

1 2 ρ L v 2 - ρ g x L - x sen ⁡ θ + x 2 sen ⁡ θ + x 2 = 0

v 2 = 2 g x L L - x sen ⁡ θ + x 2 sen ⁡ θ + x 2

v 2 = 2 g x sen ⁡ θ - x L sen ⁡ θ + x 2 L sen ⁡ θ + x 2 L

v 2 = 2 g x sen ⁡ θ + x 2 L 1 - sen ⁡ θ

E então a velocidade é:

v = 2 g x sen ⁡ θ + x 2 L 1 - sen ⁡ θ

Resposta

A velocidade dos elos é v = 2 g x sen ⁡ θ + x 2 L 1 - sen ⁡ θ .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o sistema é liberado a partir do repouso, determine as velocidades de ambas as massas após B ter se deslocado em 1m . Despreze o atrito e as massas das polias.
Quando o mecanismo é liberado a partir do repouso na posição em que θ = 60 ° , o carro de 4k g cai e a esfera de 6k g sobe. Determine a velocidade v da esfera quando θ = 180 ° . Despreze a massa das c
Um atleta de salto com vara de 80k g carregando uma vara uniforme de 4,9m e 4,5k g se aproxima do salto com uma velocidade v e ultrapassa por pouco o sarrafo colocado a uma altura de 5,5m . Quando ele
Quando o êmbolo de 5k g é liberado a partir do repouso em sua guia vertical com θ = 0 , cada mola de rigidez k = 3,5k N / m está sem compressão. As conexões são livres para deslizar através de seus cu
O cursor de 1,2k g do sistema do Prob. 3/149 é liberado a partir do repouso na posição A e desliza sem atrito ao longo da guia no plano vertical. Determine a força normal exercida pela guia sobre o cu