Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 33
Um velocista atinge sua velocidade máxima em segundos partindo do repouso com aceleração constante. Mantém então esta velocidade e termina metros no tempo total de segundos. Determine sua velocidade máxima
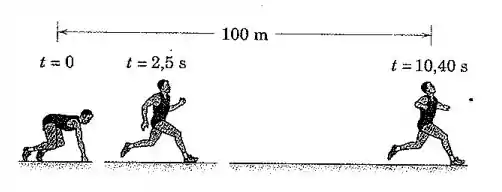
Passo 1
Vamos dizer que é intervalo de tempo em que o velocista está “acelerando”. Nesse caso:
A distância que o ciclista percorre nesse intervalo é:
E vamos dizer que é o intervalo em que o velocista mantém sua velocidade constante:
Passo 2
Agora vamos ver quais informações nós temos sobre essas grandezas:
Substituindo os valores que encontramos acim para e :
Pronto!
Resposta
A velocidade máxima do velocista é .
Exercícios de Livros Relacionados
Um carro está para ser içado por um elevador até o quarto andar de uma garagem de estacionamento que fica 14,4m acima do solo. Se o elevador pode acelerar a 0,18m / s 2 , desacelerar a 0,09m / s 2 e a
Duas partículas A e B partem do repouso na origem s = 0 e movem-se ao longo de uma linha reta de tal maneira que a A = 6 t - 3m / s 2 e a B = 12 t 2 - 8m / s 2 , onde t é dado em segundos. Determine a
O movimento de uma partícula é definido pela relação x = 5 3 t 3 - 5 2 t 2 - 30 t + 8 x , onde x e t são expressos em metros e segundos, respectivamente. Determine o tempo, a posição e a aceleração qu
O movimento de uma partícula é definido pela relação x = 12 t ³ - 18 t ² + 2 t + 5 ³ ² , onde x e t são expressos em metros e segundos, respectivamente. Determine a posição e a velocidade quando a ace
O movimento de uma partícula é definido pela relação x = 6 t ³ - 8 + 40c o s π t ³ , onde x e t são expressos em milímetros e segundos, respectivamente. Determine a posição, a velocidade e a aceleraçã