Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 121
A curva está conectada ao cano nos flanges em e como mostra a figura. Se o diâmetro de cano é e ele transmite uma descarga de , determine as componentes horizontal e vertical da reação da força e da reação do momento exercidas sobre a base fixa do apoio. O peso total da curva e da água dentro dela é , com centro de massa no ponto . A pressão da água nos flanges e é e , respectivamente. Suponha que nenhuma força é transferida aos flanges em e . O peso específico da água é .
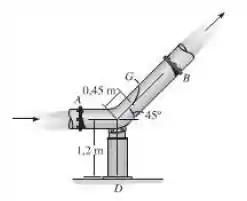
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Primeiro vamos definir as forças geradas pelas pressões:
Por definição, podemos relacionar a velocidade com a vazão:
Vamos analisar a influencia das forças:
Resposta
Exercícios de Livros Relacionados
143. O jato viaja a uma velocidade de 800 km/h, a 30° em relação à horizontal. Se o combustível está sendo gasto a 1,5kg/s, e o motor admite o ar a 200 kg/s, equanto o gás exaurido (ar e combustível )
125. O helicóptero de 10Mg carrega um recipiente contendo 500kg de água, que é usada para combater incêndios. Se ele paira sobre a Terra em uma posição fixa e, em seguida, libera 50kg/s de água a 10m/
124. O foguete tem uma massa de 32500kg, incluindo o combustível sólido. Determine em que taxa constante o combustível deve ser queimado de modo que o seu empuxo forneca ao foguete uma velocidade de 6
144. O foguete tem uma massa inicial m 0 , incluindo o combustível. Por razoes práticas de conveniência a tripulação, é necessário que ele mantenha uma aceleração ascendente constante a 0 . Se o combu
123. Um míssil tem a massa de 1,5 M g (sem combustível). Se ele consome 500kg de combustível sólido a uma taxa de 20kg/s e o ejeta com uma velocidade de 2000m/s em relação ao míssil, determine a veloc