Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 77
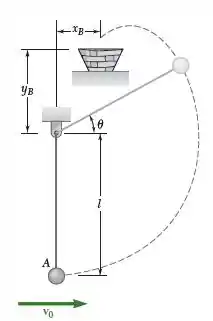
Uma bola de em é suspensa por uma corda inextensível e tem velocidade inicial de . Se e , determine de modo que a bola entre no cesto.
Passo 1
Neste problema, é necessária uma atenção extra, pois estaremos trabalhando com dois momentos no movimento.
O primeiro momento corresponde ao que chamaremos de posição , na qual a bola está inicialmente.
Sabemos que em um ponto do movimento o caminho da bola muda de circular para parabólico, pois o cabo ficará frouxo, nos dando um ponto de tensão nulo. A bola descreverá um movimento parabólico neste instante até o final quando entra no cesto.
Então vamos escrever as equações para o nosso sistema e calcular.
Temos que:
Onde é o comprimento inicial da corda e é o ângulo entre a corda e a horizontal.
Aplicando a segunda lei de Newton, temos que:
Onde indica a aceleração normal, a velocidade final da bola e a tensão. Como o cabo fica frouxo no ponto, consideramos que , logo:
Passo 2
Agora que encontramos a equação da velocidade no ponto, podemos aplicar o principio da conservação de energia com relação às duas posições.
Temos que:
Onde indica a velocidade inicial.
E:
Para a posição , temos:
E:
Passo 3
Relacionando as equações do passo anterior, temos:
Cortando os termos em comum, temos que:
Mas descobrimos que Portanto:
Logo:
Agora é só substituir os dados do enunciado:
Podemos encontrar também a velocidade na posição .
Passo 4
Agora vamos trabalhar com a posição , que é a posição em que se inicia o movimento parabólico, como a posição inicial e o momento em que a bola chega à cesta como o final.
Temos que:
A distância horizontal entre a cesta e o ponto de suspensão da bola é:
Onde é o tempo que a bola leva para chegar ao ponto e é o tempo que a bola leva para chegar ao ponto .
Substituindo os dados, temos que:
Passo 5
Vamos realizar o mesmo procedimento para , temos que:
Substituindo os valores, teremos que:
Sendo este o valor pelo qual a bola entrará na cesta.