Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 106
Após o retorno do módulo lunar ao módulo de comando, a espaçonave Apollo foi girada em torno de si mesma de modo que o módulo lunar ficou voltado para trás. O módulo lunar foi então ejetado à deriva com uma velocidade de relativa ao módulo de comando. Determine a intensidade e a direção (ângulo formado com a vertical ) da velocidade do módulo justamente antes de ele colidir com a superfície da Lua em .
Passo 1
Oi, pessoal! Tudo bem? Vamos à resolução do problema!!
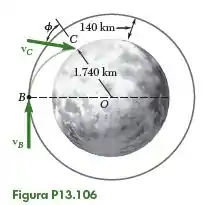
O enunciado informa que o módulo lunar foi ejetado à deriva com uma velocidade de relativa ao módulo de comando, e a figura nos fornece os seguintes dados:
Nosso objetivo é determinar a intensidade e a direção da velocidade do módulo lunar exatamente antes de ele colidir com a superfície da Lua em . Como temos a altitude do ponto e o raio da lua, vamos calcular .
Passo 2
Módulo de comando em órbita circular:
O produto , pode ser expresso conforme a Eq. 12,29:
Sabemos que,
E sendo
Substituímos os valores na equação para obtermos :
Sabemos que
Conforme a Eq. 12.28:
Então,
Sabendo que, para um satélite em órbita circular,
Temos que,
Substituindo os valores que temos, encontramos :
Em posse de e da velocidade relativa, podemos encontrar :
Passo 3
Aplicando o princípio da conservação de energia entre e :
Observe que . Fazendo as devidas substituições:
Passo 4
Já encontramos a intensidade de , agora queremos saber o ângulo que ela forma com a vertical .
Vamos aplicar o princípio da conservação do momento angular: