Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 107
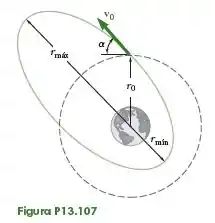
Um satélite é lançado ao espaço com uma velocidade a uma distância do centro da Terra pelo último estágio de seu foguete lançador. A velocidade foi calculada para enviar o satélite para uma órbita circular de raio . Entretanto, devido a uma falha de controle, o satélite não é lançado horizontalmente, mas a um ângulo com a horizontal e, como resultado, é propulsionado para uma órbita elíptica. Determine os valores máximo e mínimo da distância entre o centro da Terra e o satélite.
Passo 1
Oi, galerinha! Beleza?
O problema pede que determinemos os valores máximo e mínimo da distância entre o centro da Terra e o satélite, e explica que por causa de uma falha de controle, o satélite não foi lançado horizontalmente, mas a um ângulo com a horizontal.
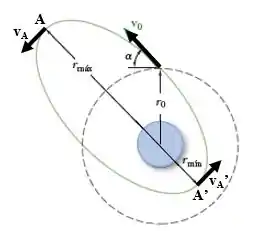
Para a orbita circular de raio :
Sabemos que, pela 2ª Lei de Newton:
Conforme a Eq. 12.28:
Então,
Sabendo que, para um satélite em órbita circular,
Temos que,
Passo 2
Aplicando o princípio da conservação do momento angular:
Agora o princípio da conservação de energia:
Passo 3
Vamos então fazer as devidas substituições:
Já encontramos uma expressão para , dessa forma:
E sabemos que
Então nossa equação ficará:
Podemos cortar de ambos os lados da equação. Nos restará:
Passo 4
Em posse da equação de 2º grau, vamos resolvê-la utilizando a fórmula de Bhaskara:
Portanto,
E