Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 109
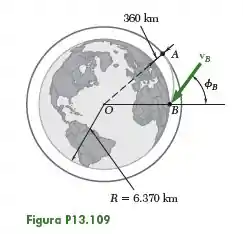
Um veículo espacial encontra-se em uma órbita circular a uma altitude de acima da Terra. Para retornar à Terra, ele diminui sua velocidade quando passa por , acionando seu motor por um curto intervalo de tempo em sentido oposto ao de seu movimento. Sabendo que a velocidade do veículo espacial deve formar um ângulo com a vertical quando ele atingir o ponto a uma altitude de , determine (a) a velocidade necessária para que o veículo deixe sua órbita circular em , (b) sua velocidade no ponto .
Passo 1
Oi, gente!! Tudo joinha?
O problema pede que determinemos a velocidade necessária para que o veículo deixe sua órbita circular em e a velocidade dele no ponto , sabendo que ela deve formar um ângulo com a vertical. O enunciado e a figura nos fornecem as seguintes informações:
Em posse das altitudes dos pontos e e do raio da Terra, podemos calcular e :
Aplicando o princípio da conservação do momento angular:
Passo 2
Calculando a energia cinética e potencial.
Ponto A:
Aplicando agora a Eq. 13.17, usada para a energia potencial quando a variação da força da gravidade não pode ser desprezada:
O produto , pode ser expresso conforme a Eq. 12,29:
E sendo
Substituímos os valores na equação para obtermos :
Substituindo na Eq. 13.17:
Ponto B:
Passo 3
Em posse das energias cinética e potencial, vamos aplicar o princípio da conservação da energia:
Sabemos que
Então,
Agora só substituir em
Prontinho, temos as duas velocidades solicitadas!