Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 105
Uma espaçonave descreve uma órbita elíptica em torno da Terra com uma velocidade máxima em e uma velocidade mínima em . Determine a altitude da espaçonave em .
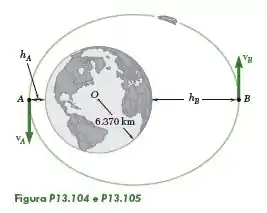
Passo 1
Olá, galera! Tudo bem?
O problema pede que determinemos a altitude da espaçonave em , e nos fornece as altitudes mínima e máxima como dados:
Aplicando o princípio da conservação do momento angular:
Como a massa está presente em ambos os lados, então:
Passo 2
Calculando a energia cinética e potencial.
Ponto A:
Aplicando agora a Eq. 13.17, usada para a energia potencial quando a variação da força da gravidade não pode ser desprezada:
No caso de um corpo de massa sujeito à atração gravitacional da Terra, o produto , pode ser expresso de acordo a Eq. (12.29),
em que e são, respectivamente, a massa e o raio da Terra.
Sabemos que,
e
Então, substituindo na Eq. (12.29), temos,
Substituindo em :
Ponto B:
Aplicando a Eq. 13.17:
Passo 3
Em posse das energias cinética e potencial, vamos aplicar o princípio da conservação da energia:
Sabemos que
Então,
Passo 4
Agora sim podemos calcular a altitude da espaçonave em !