Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 31

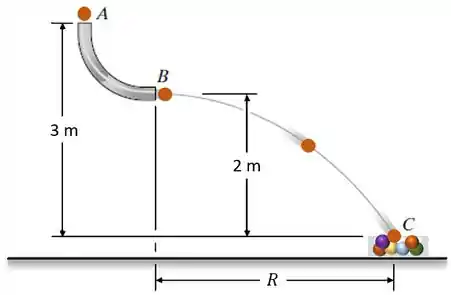
Bolas de gude tendo massa de 5 g caem do repouso em A através do tubo de vidro e se acumulam na vasilha em C . Determine a posição R da vasilha no fim do tubo e a velocidade na qual as bolas de gude caem dentro da vasilha. Despreze a dimensão da vasilha.

Passo 1

O enunciado nos dá os seguintes dados:

Massa da bola: m = 5   g = 0,005   k g ;

Altura do ponto A : h A = 3 m;

Altura do ponto B : h B = 2 m.

Além disso, sabemos que as bolas de gude caem do repouso, logo, v A = 0   m / s .

Devemos determinar a a posição R da vasilha e a velocidade na qual as bolas de gude caem dentro dela.

Vamos desenhar o diagrama de corpo livre da bola ao sair do tubo:

A única força que age sobre ela neste momento é a força peso W = m g .

Passo 2

Primeiramente, vamos determinar a velocidade da bola de gude ao sair do tubo de vidro ( v B ).

Utilizando o Princípio do Trabalho e Energia, temos que

T A + ∑ U A - B = T B

onde

T A = 1 2 m v A 2 = 1 2 m 0 2 = 0

T B = 1 2 m v B 2 = 0,00 5 v B 2 2

∑ U A - B = W y A - B = m g h A - h B = 0,00 5 g

Substituindo esses valores na equação inicial, obtemos

0 + 0,00 5 g = 0,00 5 v B 2 2

v B 2 = 2 g = 19,62

v B = 4,429   m / s

Como podemos ver no desenho do enunciado, esta velocidade será somente horizontal, ou seja, ela não possui componente no eixo y .

Passo 3

Agora que sabemos a velocidade em B , podemos encontrar o valor de R utilizando as seguintes equações conhecidas para o eixo y e x , respecticamente, utilizando os valores das propriedades no ponto B como referência:

s = s 0 + v 0 t + 1 2 a t 2

s = s 0 + v 0 t

No eixo y :

s = s 0 + v 0 t + 1 2 a t 2

- 2 = 0 + 0 - 1 2 g t 2

t = 0,6386   s

No eixo x :

s = s 0 + v 0 t

R = 0 + 4,429 0,6386

R = 2,83   m

Passo 4

Em seguida, vamos aplicar o Princípio do Trablho e Energia entre os ponto A e C para encontrar o valor de v C .

Temos que

T A + ∑ U A - C = T C

onde

T A = 1 2 m v A 2 = 1 2 m 0 2 = 0

T C = 1 2 m v C 2 = 0,00 5 v C 2 2

∑ U A - B = W y A - C = m g h A - h C = 0,015 g

Substituindo esses valores na equação inicial, obtemos

0 + 0,015 g = 0,00 5 v C 2 2

v C 2 = 6 g = 58,86

v C = 7,67   m / s

Resposta

R = 2,83   m

v C = 7,67   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bola de 0,5 kg de dimensão desprezível é lançada para cima na pista circular vertical lisa usando o pistão com mola. O pistão mantém a mola comprimida 0,08 m quando s = 0 . Determine até que s ele d
A caixa de 1 kg desliza na rampa circular lisa. Se a caixa tem uma velocidade de 9 m/s em A , determine a velocidade da caixa e a força normal atuando sobre a rampa quando a caixa está localizada em B
Pacotes tendo massa de 25 kg são passados para a calha de escoamento a v A = 0,9 m/s utilizando-se uma calha transportadora. Determine suas velocidades quando eles chegam aos ponts B , C e D . Calcule
O motor a diesel de um trem de 400 Mg aumenta a velocidade do trem uniformemente do repouso para 10 m/s em 100 s ao longo de uma ferrovia horizontal. Determine para potência média desenvolvida.
Se o coeficiente de atrito cinético entre a caixa de 100 kg e o plano é μ k = 0,25 , determine a compressão x de mola necessária para levar a caixa instantaneamente ao repouso. Inicialmente, a mola nã