Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 46
O motor de um carro de massa 1750 kg está gerando uma potência constante de 37,5 kW enquanto o carro está se deslocando em uma aclive com velocidde constante. Se o motor está operando com uma eficiência de , determine a velocidade do carro. Despreze o arrasto e a resistência ao rolamento.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do carro: ;
Potência constante: ;
Eficiência do motor: .
Devemos determinar a velocidade constante do carro sabendo que o motor tem uma eficiência de .
Como o carro está em um declive, vamos desenhar o diagrama de corpo livre para poder visualizar melhor a ação das forças sobre ele:
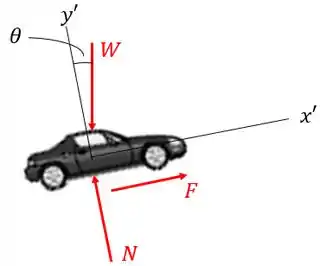
Onde é a fora peso, é a força normal e é a força exercida pelo motor pra fazer com que o carro suba o declive.
A tangente do ângulo será igual a
Logo,
Passo 2
Primeiramente, vamos utilizar a Equação do Movimento para encontrar o valor da força .
No eixo :
Passo 3
Pror definição, sabemos que a potência é dada pela seguinte fórmula
A questão nos diz que o motor exerce uma potência W. Está é a potência de entrada do motor. Devemos descobrir a potência de saída para poder encontrar a velocidade.
Para isso, devemos considerar a eficiência .
Por definição, temos que
Logo,
Substituindo este valor na fórmula da potência , obtemos