Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 178
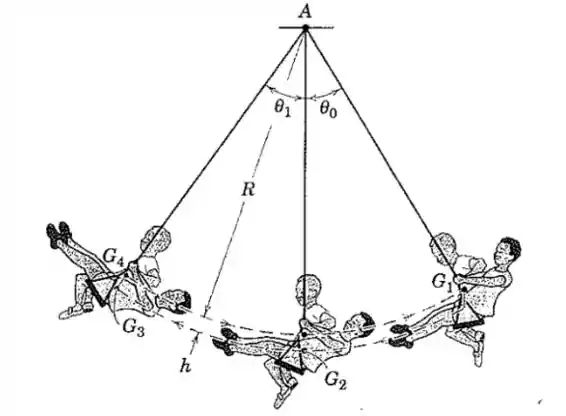
“Bombeando” enquanto balança, o menino aumenta a amplitude de oscilação de para pela variação abrupta da posição de sentado para a de deitado de costas no início de cada oscilação pra frente e invertendo as posições no início de cada oscilação para trás. Considere o menino como uma partícula em cada uma das duas configurações onde a trajetória do seu centro de massa é mostrada pela linha tracejada. Qualquer perda de energia mecânica entre e pode ser considerada como sendo desprezível. Expresse em termos de , e .
Passo 1
O trajeto que o menino faz o seguinte trajeto:
A lei de conservação de energia vale para qualquer par de pontos que quisermos:
Vamos aplicar isso aos pontos e , que são os pontos de retorno na oscilação do menino:
E o jeito mais fácil de resolver essa questão é lembrar que nos limites das trajetórias a velocidade é nula, porque o menino para antes de começar a retornar. Então:
Passo 2
Agora vamos tentar escrever as energias potenciais nesses dois pontos, considerando que a energia é zero no ponto :
E agora podemos calcular as “alturas” desses pontos em relação ao ponto para calcular as energias potenciais:
E então:
Resposta
O ângulo é .