Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 63
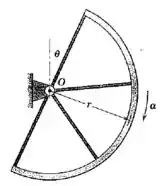
O anel semicircular uniforme de massa e raio médio está montado sobre raios de massa desprezível e gira em torno de um eixo horizontal através de . Se o anel é liberado a partir do repouso na posição , determine a força suportada pelo mancal imediatamente após a liberação.
Passo 1
O primeiro passo é encontrar a aceleração angular do anel nessa posição. O único momento agindo sobre ele é o da força peso, que age no centro de massa, a uma distância do ponto :
E podemos consultar uma tabela para encontrar tanto a posição quanto o momento de inércia :
Então:
Passo 2
E agora vamos analisar as duas componentes (normal e tangencial), para encontrar as forças e .
Primeiro aplicamos a segunda lei de Newton na direção tangencial, as únicas forças que agem nessa direção são a componente tangencial do peso e a força no mancal:
Agora vamos substituir com os valores que já temos:
E podemos fazer praticamente a mesma coisa na direção normal, mas dessa vez a resultante deve se anular:
Dessa vez ficamos com a outra componente da força peso e a força na direção centrípeta:
Passo 3
E agora já podemos calcular o módulo total da força :
Resposta
A força suportada pelo mancal é .