Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 64
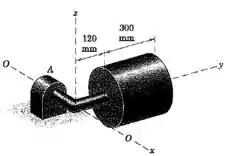
O cilindro maciço homogêneo possui uma massa de e está montado em um eixo em ângulo reto que gira livremente em torno do eixo horizontal -. Se o cilindro é liberado a partit do repouso com o seu eixo no plano horizontal, calcule a aceleração angular inicial do conjunto e a força resultante exercida pelo mancal sobre o eixo. A massa do eixo pode ser desprezada.
Passo 1
O primeiro passo é encontrar a aceleração angular do cilindro assim que é liberado. Para isso precisamos do momento de inércia em relação ao eixo horizontal -. Para isso vamos precisar do teorema dos eixos paralelos:
E podemos consultar (paralelo ao eixo ) em uma tabela:
E a distância entre o centro de massa do cilinro e o eixo de rotação é:
Então:
O raio do cilindro (apesar de estar parcialmente encoberto no desenho do enunciado) foi dado, e vale :
Passo 2
Agora vamos ver a equação que relaciona esse momento à aceleração angular:
E a única força que produz momento em relação ao ponto é a força peso do cilindro, que age sobre o centro de massa, a uma distância do eixo de rotaçao.
E podemos usar isso para encontrar a aceleração do centro de massa, e então poderemos escrever equações para a força resultante sobre o cilindro:
Passo 3
Agora podemos aplicar a segunda lei de Newton para encontrar a força exercida pelo mancal sobre o eixo. É de esperar que essa força aponte na direção positiva do eixo :
Imediatamente após ser liberado a partir do repouso, a aceleração do centro de massa do cilindro também aponta exatamente nessa direção, então:
Resposta
A força resultante exercida pelo mancal nesse instante é .