Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 56
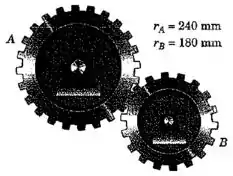
A massa da engrenagem é de e seu raio de giração centroidal é de . A massa da engrenagem é de e seu raio de giração centroidal é de . Calcule a aceleração angular da engrenagem quando um torque de é aplicado ao eixo da engrenagem . Despreze o atrito.
Passo 1
Quais são os momentos que agem sobre a engrenagem em ? Temos o momento favorecendo a rotação em uma direção, e a força de contato com a outra engrenagem favorecendo a rotação na direção oposta.
E podemos relacionar isso à aceleração angular da engrenagem através do momento de inércia:
E podemos escrever esse momento de inércia em função do raio de giração.
E então:
Passo 2
Agora faremos a mesma coisa para a engrenagem . Nesse caso o único momento agindo sobre a engrenagem é o associado à força de contato entre as engrenagens.
Aí já temos duas equações e três variáveis (, e ), então precisamos de mais uma equação para poder resolver o problema.
Como as duas engrenagens estão em contato as suas acelerações tangenciais têm que ser iguais (é impossível que uma delas acelerece sozinha):
Agora sim, temos um sistema de três variáveis e três equações:
Passo 3
Para resolver esse sistema, primeiro vamos multiplicar as duas primeiras equações por :
Agora vamos substituir a segunda na primeira para encontrar o seguinte:
E agora substituímos isso na terceira:
E colocando esse resultado na primeira equação:
Resposta
As acelerações angular são e .