Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 59

O braço e o assento de uma atração de parque de diversões têm massa de 1,5 Mg, com o centro de massa localizado no ponto G 1 . O passageiro sentado em A tem massa de 125 kg, com o centro de massa localizado em G 2 . Se o braço é levantado a uma posição em que θ = 150 ° , e em seguida liberado do repouso, determine a velocidade do passageiro no instante θ = 0 ° . O braço tem raio de giração k G 1 = 12   m , em relação a seu centro de massa G 1 . Despreze a dimensão do passageiro.

Passo 1

Iremos considerar a aceleração da gravidade g = 9,81   m / s 2 .

Para a resolução do exercício, tomaremos como base o diagrama a seguir:

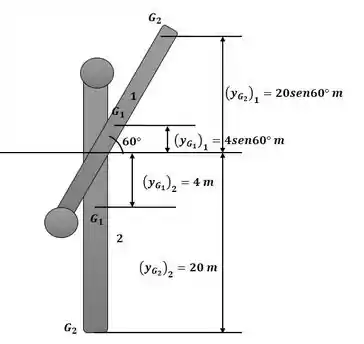
Sendo assim, analisaremos primeiro a energia potencial do sistema com relação ao eixo de referência:

V 1 = V g 1 = W 1 y G 1 1 + W 2 y G 2 1

V g 1 = 1500 9,81 4 s e n 60 ° + 125 ( 9,81 ) ( 20 s e n 60 ° )

V g 1 = 72213,5   J

V 2 = V g 2 = - W 1 y G 1 2 - W 2 y G 2 2

V g 2 = - 1500 9,81 4 - 125 ( 9,81 ) ( 20 )

V g 2 = - W 1 y G 1 2 - W 2 y G 2 2

V g 2 = - 83385   J

Passo 2

Agora iremos analisar a energia cinética do sistema, mas antes disso, iremos escrever as velocidades em G 1 e G 2 e seu momento de inércia com relação a G 1 :

v G 1 = ω r G 1 = ω ( 4 )

v G 2 = ω r G 2 = ω ( 20 )

I G 1 = m 1 k G 1 2 = 1500 12 2 → I G 1 = 216000   k g . m 2

Sendo assim, a conservação da energia cinética do sistema é dado por:

T = 1 2 m 1 v G 1 2 + 1 2 I G 1 ω 2 + 1 2 m 2 v G 2 2

T = 1 2 1500 ω 4 2 + 1 2 216000 ω 2 + 1 2 125 ω 20 2

T = 145000 ω 2

Sabendo que o sistema está inicialmente em repouso, T 1 = 0 .

Passo 3

Com isso, podemos aplicar a conservação de energia para o sistema:

T 1 + V 1 = T 2 + V 2

0 + 72213,53 = 145000 ω 2 - 83385

ω = 1,036   r a d / s

Sendo assim, a velocidade é dada por:

v = ω r = 1,036 20 → v = 20,7   m / s

Resposta

v = 20,7   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo AB forma um quarto de círculo de raio médio r contém uma corrente lisa cuja massa por unidade de comprimento é m a . Se a corrente é solta do repouso da posição mostrada, determine a sua veloc
Se a massa da Terra é M e , mostre que a energia potencial gravitacional de um corpo de massa m localizado uma distância r do centro da Terra é: V s =- G M e m / r Lembre-se de que a força gravitacion
Um volante de 1200k g com um raio de giração de 400m m tem sua velocidade reduzida de 5000 para 3000r p m durante um intervalo de 2m i n . Calcule a potência média fornecida pelo volante. Expresse a s
Um pequeno veículo experimental possui uma massa total m de 500k g , incluindo as rodas e o piloto. Cada uma das quatro rodas tem uma massa de 40k g e um raio de giração centroidal de 400m m . A resis
49. A porta da garamgem CD tem massa de 50 kg e pode ser tratada como uma placa fina. Determine o comprimento não deformado requereido de cada uma das duas molas laterais quando a porta estiver na pos