Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 145 (b)

Um pequeno veículo experimental possui uma massa total m de 500   k g , incluindo as rodas e o piloto. Cada uma das quatro rodas tem uma massa de 40   k g e um raio de giração centroidal de 400   m m . A resistência por atrito total R para o movimento é de 400   N e é medida rebocando o veículo a uma velocidade constante em uma estrada horizontal com o motor desengrenado. Determine a potência fornecida pelo motor para uma velocidade de 72   k m / h subindo a inclinação de 10 % (a) com aceleração nula e (b) com uma aceleração de 3 m / s ² .

Passo 1

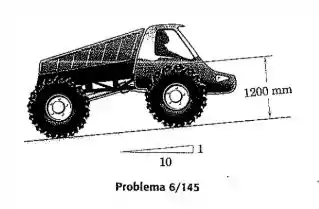
A inclinação θ da estrada é dada por

θ =   t g - 1 1 10 = 5,711 °

Vamos seguir a sugestão do enunciado, que afirma que a potência equivale à taxa de aumento no tempo da energia total do veículo ascrescida da taxa em que o trabalho devido ao atrito é superado. Equacionando, temos

P = d U d t = d d t T + V g + R v  

Substituindo as expressões para variação de energia cinétia e potencial gravitacional:

d U d t = d d t ∑ 1 2 m v 2 + d d t ∑ 1 2 I - ω 2 + R v

Aplicando a regra da cadeia e resolvendo as derivadas, ficamos com

P = m v a + 4 I - ω α + m g v s e n θ + R v

Passo 2

Da equação encontrada para a potência, se isolarmos a aceleração a ficamos com

P = ( m v + 4 I - ω ) a + m g v s e n θ + R v

Tomando a =   3 m s 2 , a potência fornecida pelo motor é

P = 500 72 3,6 + 4 40 0,4 2 72 3,6 0,6 2 3 + 17761

Resolvendo para P, achamos

P = 52,027   k W

Resposta

a = 3 m s 2       →       P = 52,027 k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As molas estão sem deformação na posição indicada. Se o cursor de 6k g é liberado a partir do repouso na posição em que a mola inferior é comprimida de 125m m , determine a compressão máxima x B da mo
O sistema é liberado a partir do repouso na posição indicada. O cilindro de 6k g passa através do furo na cantoneira, mas o disco de 4k g não. Determine a altura máxima h que o cilindro de 8k g sobe.
O cursor C de 2k g com a mola conectada se desloca com atrito de A até B ao longo da haste fixa. Se o cursor tem uma velocidade de 3m / s em A e uma velocidade de 5m / s em B , determine a perda U f d
O ponto fixo O é localizado em um dos dois focos da guia elíptica. A mola tem uma rigidez de 3N / m e não está esticada quando o cursor está em A . Se a velocidade v A é tal que a velocidade do cursor
Se o sistema é liberado a partir do repouso, determine as velocidades de ambas as massas após B ter se deslocado em 1m . Despreze o atrito e as massas das polias.