Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 108
O braço curvo e os cabos e presos a ele sustentam uma linha de transmissão, que está situada no plano vertical -. As tangentes à linha de transmissão, na posição do isolante abaixo de , fazem ângulos de com o eixo horizontal . Se a força trativa na linha, na posição do isolante, vale , calcule a força total suportada pelo parafuso em no suporte do poste. O peso do braço pode ser desprezado comparado com as outras forças e pode-se assumir que o parafuso em suporta apenas força horizontal.
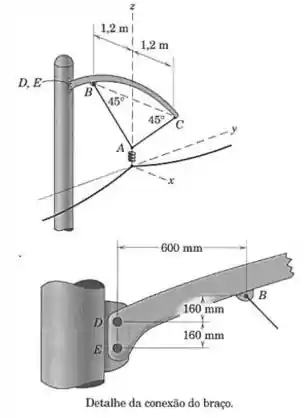
Passo 1
Vamos pensar no braço curvo e nos cabos e como um sistema, e então pensar nas forças externas que atuam sobre ele.
A primeira dessas forças é a que age sobre o isolante em , através da tensão nos fios. Em cada um dos lados temos uma força de formando um ângulo de com o eixo .
E então a força que os cabos exercem sobre o ponto é:
E essa é a força que, no final das contas, tem que ser suportada pelos apoios em e .
Passo 2
Como o enunciado diz que a força no parafuso em é apenas horizontal, nós sabemos que a força terá que ser compensada inteiramente pelo parafuso em , ou seja:
Onde é a componente da força na direção do eixo . Isso é uma consequência da equação de equilíbrio das forças nessa direção .
Agora falta encontrar a outra componente da força em .
Passo 3
Vamos desenhar a situação dos parafusos:
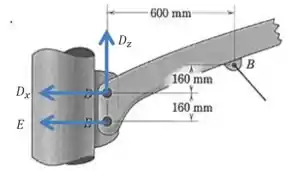
Vamos calcular o momento em relação ao ponto :
A força terá momento nulo, já que está sobre o nosso ponto de referência. A força tem uma linha de ação que cruza o ponto , então também tem momento nulo.
A força está a (distância perpendicular) do ponto , e favorece a rotação no sentido anti-horário, e a força está a de distância do ponto, e favorece a rotação no sentido anti-horário também.
E o sinal negativo indica que a força aponta no sentido contrário ao que nós representamos no desenho!
E então o módulo da força é:
Resposta
A força suportada pelo parafuso é .