Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas Fundamentais - Ex. 10
Determine a tração desenvolvida nos cabos AB, AC e AD.
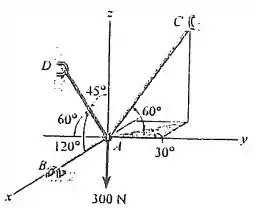
Passo 1
Falaaa!
Para encontrar o valor da tração em cada cabo, o que deve ser feito primeiramente é o diagrama de corpo livre no qual serão representadas as forças envolvidas na tração.
Logo, fazendo o diagrama de corpo livre tem-se:
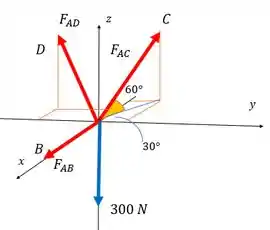
E, então, observando o desenho feito consegue-se montar as equações de equilíbrio.
O equilíbrio de forças deve ser analisado nas três dimensões x, y e z, pelo fato de as forças estarem atuando em todos esses três sentidos.
Passo 2
Para fazer o somatório de forças em cada eixo, precisamos decompor as nossas forças nos eixos coordenados:
- A força de está na direção de , então ela só tem componente nesse eixo e vale mesmo.
- A força está na direção positiva do eixo . Então ela também só tem componente em um eixo:
- A força faz um ângulo de com o plano . A componente dela, vai ser
Já que esse ângulo é oposto ao eixo . Para achar as outras componentes a gente precisa achara projeção dessa força em , assim:
Aí as componentes de e serão as projeções desse carinha. Temos que essa projeção faz com o eixo . Nesse caso, a componente vai ser a força projetada vezes cosseno de . E a em a gente usa seno. E repara que vai estar no sentido negativo e no positivo.
E para , o que ele quer dizer é que essa força faz um ângulo de com eixo e um ângulo de com eixo . Para achar a componente das forças nesses eixos, é só multiplicar a força por cosseno do ângulo entre a força e o eixo referido.
Aí fica:
E ela faz um ângulo de com a parte negativa de , então a gente faz algo parecido, mas bota o sinal de menos:
Passo 3
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo, ou seja:
Adotando o sentido dos eixos mostrado no desenho do enunciado:
Passo 4
Agora, como há três equações encontradas, é possível montar um sistema de equações e determinar a solução dele, cuja solução será o valor das forças.
Resolvendo este sistema, obtem-se: