Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas Fundamentais - Ex. 7
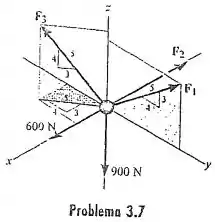
Determine as intensidades das forças , de modo que a partícula seja mantida em equilíbrio.
Passo 1
Para encontrar os valores das forças, o que deve ser feito primeiramente é o diagrama de corpo livre. Em seguida, o equilíbrio de forças deve ser analisado nas três dimensões x, y e z pelo fato de as forças estarem atuando em todos esses sentidos.
Passo 2
Logo, fazendo o diagrama de corpo livre tem-se:
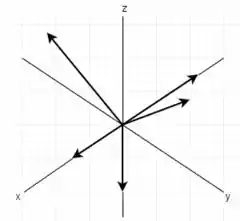
E, então, observando o desenho feito consegue-se montar as equações de equilíbrio.
Passo 3
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo, ou seja:
Adotando o sentido dos eixos mostrado no desenho do enunciado:
Passo 4
Agora, como há três equações encontradas, é possível montar um sistema de equações e determinar a solução dele, cuja solução será o valor das forças.
Resolvendo este sistema, obtem-se: