Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 82
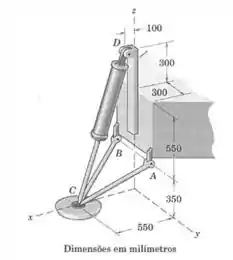
Um dos três trens de aterrissagem de uma nave proposta para pousar em Marte está mostrado na figura. Como parte de uma verificação do projeto sobre a distribuição de força na estrutura de aterrissagem, calcule a força em cada um dos elementos , e quando a nave está em repouso sobre uma superfície horizontal em Marte. O arranjo é simétrico em relação ao plano -. A massa da nave é de . (Considere que os trens de aterrissagem suportam cargas iguais e consulte a Tabela no apêndice quanto necessário).
Passo 1
O primeiro passo é descobrir qual é a força a ser suportada pelo trem de aterrissagem. O peso da nave está dividida igualmente entre os três trens, e é preciso lembrar que temos que considerar a aceleração da gravidade em marte:
Consultando a tabela que foi indicada no enunciado encontramos :
E escrevendo em forma vetorial, é a força de reação que deve existir entre o chão e o pé.
Passo 2
Agora vamos escrever expressões vetoriais para as forças , e , para isso precisamos de vetores unitários em cada uma dessas direções (olhe para o desenho para entender essa parte):
E agora cada uma daquelas forças é simplesmente um valor , ou multiplicado pelo respectivo vetor unitário.
Passo 3
Agora que já temos tudo escrito na forma vetorial, podemos aplicar a condição de equilíbrio:
Mas podemos simplificar um pouco isso se lembrarmos que o enunciado afirmou que o sistema é simétrico em relação ao plano , isso quer dizer que:
E para que essa soma vetorial seja nula, todas as componentes tem que ser iguais a zero:
Pela primeira equação temos:
E substituindo isso na segunda:
E agora voltando na equação de antes:
Passo 4
Por que os sinais negativos? Eles indicam que a direção dos vetores é diferente da direção dos vetores unitários que nós escrevemos:
E então as respostas finais são:
Resposta
As forças são , e .