Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 134
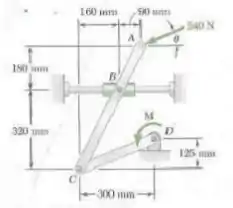
O braço está ligado por pinos ao colar em e à manivela em . Desprezando o efeito do atrito, determine o binário necessário para manter o sistema em equilíbrio quando .
Passo 1
Desejamos encontrar o valor do momento de binário representado por de tal forma que o sistema fique em equilíbrio quando . Assim, tomemos o diagrama de corpo livre para
Utilizando as equações de equilíbrio vamos ter
Passo 2
Agora, tomemos o diagrama de corpo livre para o membro teremos
Adotando o sentido anti-horário como positivo teremos
Resposta
Exercícios de Livros Relacionados
A esfera lisa e homogênea de 50k g está apoiada em uma rampa a 30 ° em A e apoiada contra a parede vertical lisa. Determine as forças de contato em AeB .
Um carpinteiro segura uma tábua uniforme com 6 kg, como mostrado. Determine as formas emAeB, se ele aplica forças verticais à tábua.
A viga uniforme tem uma massa de 50 kg por metro de comprimento. Calcule as reações no apoioO. Determine as reações nos suportes.
A viga com carga uniforme de 500 kg é submetida aos três carregamentos externos, como mostrado. Calcule as reações no pontoOdo suporte.
A massa da bicicleta é de 13 kg com centro de massa emG. Determine as forças normais emAeBquando a bicicleta está em equilíbrio.