Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 4
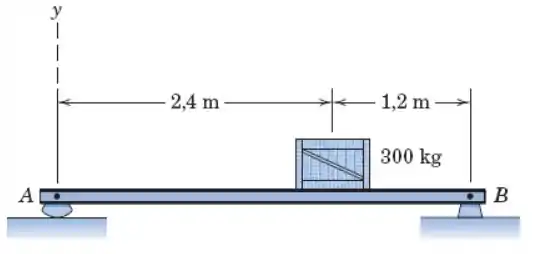
A viga uniforme tem uma massa de 50 kg por metro de comprimento. Calcule as reações no apoio O. Determine as reações nos suportes.
Passo 1
E aí meus queridxs, tudo bom com vocês?
Se liga só, vamos direto ao ponto aqui porque a questão é bastante simples e tranquila de ser feita. Primeiro de tudo vamos desenhar as reações de apoio das quais o enunciado trata, né? Pois bem, ficaremos com o seguinte diagrama de forças
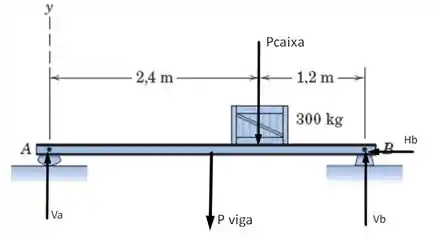
Passo 2
Agora que desenhamos todas as forças que atuam no nosso sistema ficou fácil, vamos apenas aplicar as equações de equilíbrio estático que é nada mais nada menos do que pegar a resultante das forças em cada direção e o momento e igualar a . Assim, temos para o eixo
Analogamente para o eixo teremos
Agora, adotando o sentido anti-horário como positivo e calculando o momento em relação ao ponto teremos
Para acharmos basta substituirmos o valor que acabamos de encontrar em , então obteremos
Pronto, tá resolvido nosso problema.